Lakatos Imre az egyik legjelentõsebb magyar származású matematika- és tudományfilozófus volt. Életpályáját itt nem tárgyaljuk, ám a megadott irodalomjegyzék kellõ támpotot szolgáltat az érdeklõdõk számára. Annyit elég elmondanunk, hogy 1956 és 1960 között Cambridge-ben tartózkodott, és itt írta meg (második) doktori disszertációját, a matematikatörténet-matematikafilozófia témakörébõl. Ennek a munkának egy részlete megjelent könyv alakban, és ez magyarul is olvasható Bizonyítások és cáfolatok címmel [1] . Ezután Londonba került Karl Popper, az egyik legnagyobb hatású huszadik századi tudományfilozófus tanszékére, ahol, eltekintve néhány korai cikktõl, elsõsorban a természettudományok történetével és filozófiájával foglalkozott. A hetvenes évek elején ismét közelíteni kezdett a matematikához, és a jelek arra utalnak, hogy a matematika és a természettudományok filozófiáját egy egyésges fogalmi keretbe kívánta rendezni. Ebben a munkában azonban megakadályozta váratlan halála.

Lakatos viszonylag kevés írással gazdagította a filozófiai irodalmat (és ezek közül sem pulblikálta mindet), ám abban egyetértés uralkodik, hogy ez a kevés óriási hatást gyakorolt a matematikafilozófiára, és még inkább a tudományfilozófiára általában. (Lásd az irodalomjegyzéket.) Mi itt csupán a matematikafilozófiájára és az ezzel kapcsolatos írásaira fogunk összpontosítani, azzal a céllal, hogy egy általános képet próbáljunk nyújtani Lakatos matematikával kapcsolatos felfogásáról. Ehhez azonban elõször megpróbáljuk felvázolni azt a matematikafilozófiai hátteret, amely elõtt Lakatos a saját munkásságát elhelyezte, és amelyhez képest elgondolásait egy ígéretesebb alternatívaként tüntette fel.

A deduktív tudományok alaptípusai

 
Annak érdekében, hogy a matematika helyét meg tudja határozni a tudományok között, Lakatos a tudományokat, vagyis az (“ideális” esetben) axiomatikus-deduktív rendszereket megpróbálta osztályozni. A finomabb megkülönböztetésektõl eltekintve itt most a két fõ típust, vagy mondhatni két fõ pólust szeretném tárgyalni: az eukleidészi rendszert, illetve a kváziempirikus rendszert.

 

Az “eukleidészi” rendszer	A “kvázi-empirikus” rendszer

 

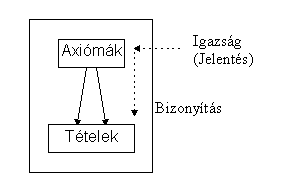
A két rendszerben közös maga az axiomatikus-deduktív jelleg, vagyis az, hogy mindkettõ bizonyos alapállításokból indul ki, és ezekbõl logikai dedukció segítségével más állításokat vezet le. A különbség abban áll, hogy milyen módon jut igazságértékhez a rendszer, vagyis mi alapján mondjuk, hogy a rendszer leír valamit.

Az eukleidészi tudományok esetén az igazság “legfelül”, az axiómák szintjén jut a rendszerbe, és innen “áramlik” lefelé, a levezetett tételek felé, hiszen a deduktív következtetés természete olyan, hogy a premisszák igazsága esetén a konklúzió igazsága automatikusan következik. Az igazságnak ezen szigorú, tévedhetetlen öröklõdését a levezetés mentén nevezhetjük bizonyításnak. Feltételezve, hogy az axiómák igazsága adott, a rendszer egészének igazsága és érvényessége megkérdõjelezhetetlen. Megjegyzendõ, hogy az eukleidészi rendszer deduktív “csatornái” nemcsak “igazság-megõrzõek”, hanem “jelentés-megõrzõek” is, vagyis a terminusok jelentése is az axiómák szintjén (definíciókkal) jut a rendszerbe, és öröklõdik a következtetések mentén.

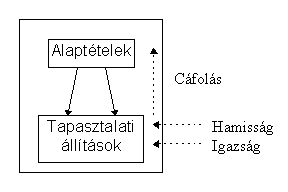
Ezzel szemben a kváziempirikus rendszerek esetén az igazság a (tág értelemben vett) tapaszatattal történõ összevetésbõl származik, azaz a legvégsõ, levezetett állítások azok, melyeknek az igazságértéke közvetlenül megállapítható. A deduktív következtetés azonban olyan, hogy irányával szemben, vagyis “felfelé” az igazság nem öröklõdhet, hiszen a konklúzió igazsága esetén nem tudjuk eldönteni a premisszákról, hogy igazak-e vagy hamisak. (Ezt úgy is meg lehet fogalmazni, hogy az indukció mûvelete egy deduktív tudomány-séma mellett nem legitim. Kivéve – bizonyos értelemben – a valószínûségi induktív logikában, amely azonban csak “valószínûleg” igaz, ezért nem adhat számot a tudományos tudás kognitív bizonyosságáról.) A hamisság azonban öröklõdik felfelé, hiszen egy logikai következtetés hamis konklúziója maga után vonja a premisszák “hamisságát”, azaz hogy a premisszák egyszerre nem tehetõk igazzá. Ezért aztán a kváziempirikus rendszerek cáfoló jellegûek. (Ezt a nézetet, miszerint egy tapasztalati tudomány elméletei sosem bizonyíthatók a tapasztalat segítségével, hanem csak cáfolhatók, Lakatos a már említett Karl Poppertõl tanulta.) Itt is meg kell jegyeznünk, hogy a jelentés szintén nem képes “felfelé áramlani”, ezért aztán a kváziempirikus tudományok esetén jóval nagyobb szabadság áll rendelkezésre a terminusok jelentésével kapcsolatban, mint az eukleidészi tudományoknál. Ennek késõbb komoly jelentõsége lesz, hiszen kiderül, hogy a matematika inkább e második csoportba tartozik.

De hogyan lehetséges, hogy a matematika nem az eukleidészi jelleget mutatja? Kultúránk történetének legnagyobb részében a matematikára úgy tekintettek, mint az eukleidészi tudományok mintaképére, és mint a ráció azon erõdítményére, ahonnan kiindulva talán végképp meghódítható az eukleidészi tudományok számára az emberi tudás egésze. Feltételezve azonban, hogy a matematika eukleidészi tudomány, számot kell tudnunk adni arról a mechnizmusról, amely az axiómák igazságát szolgáltatja, vagyis amelybõl a matematika abszolút bizonyossága származik. Lakatos fõként két különbözõ eukleidészi matematika-felfogást vizsgál meg, a logicizmust és a formalizmust.

Az eukleidészi matematikafilozófiák kudarca
 

A logicista filozófusok (elsõsorban Gottlob Frege és a fiatal Bertrand Russell) szerint a matematikai axiómák bizonyossága a logikai intuícióból származik. Ez azt jelenti, hogy a matematika axiómái tulajdonképpen logikailag igaz állítások, tagadásuk pedig önellentmondás. Ekkor a matematika tételeinek igazsága ugyanabból a forrásból táplálkozik, mint a matematikai bizonyítások helyessége, vagyis a logikából, ami viszont szoros kapcsolatban áll a gondolkodás alapmûveleteivel, vagyis megkérdõjelezhetetlen. A matematika tehát valóban tévedhetetlen tudomány.

A logicista program kudarca azonban hamar megmutatkozott, és a sors iróniája, hogy éppen leglelkesebb képviselõje, Russell tapintott rá egy olyan pontra (Russell-paradoxon), amely a fregei rendszer tarthatatlanságát mutatta. Az a “logikai intuíció”, amelyre a matematikát vissza akarták vezetni, és amelyet a naiv halmazelmélet foglal fogalmi keretbe, menthetetlenül ellentmondásos. Az ellentmondásokat ugyan ki lehet küszöbölni egy axiomatikus halmazelmélet segítségével, ez a lépés azonban már a logicista program elárulását jelenti: a halmazelmélet axiómáit sokkal kevésbé támasztja alá bármilyen logikai “intuíció”, mint például az aritmetika axiómáit, vagyis a matematika alaptételeinek igazolásához ez az út nem bizonyult járhatónak.

A következõ, és Lakatos szerint remélhetõleg az utolsó próbálkozás a matematika eukleidészi jellegének kimutatására David Hilbert formalista programja volt. Ha a logicista program kudarcát az ellentmondások okozták, akkor legfõbb feladatunk abban áll, hogy a matematika makulátlan testét megtisztítsuk az ellentmondásoktól. A formalista filozófia azonosítja a matematikai elméleteket formális szintaktikai kalkulusokkal, melyekkel szemben két fõ követelményt támasztunk: (1) a kalkulus ellentmondásmentes legyen (ez a követelmény tulajdonképpen helyettesíti az igazság követelményét, és ebben az értelemben a Hilbert-program nem egyértelmûen eukleidészi – annyiban viszont igen, hogy a matematikát tisztán bizonyító tudománynak látja), és (2) a kalkulus teljes legyen, vagyis minden megfogalmazható tételt bizonyítani vagy cáfolni tudjunk benne, és le tudjunk benne vezetni minden olyan állítást, amelyet kevésbé “szigorú” megfontolások alapján korábban igaznak ítéltünk.

E program kudarcára – Lakatos szerint – 1931-ben derült fény, amikor is Kurt Gödel két híres nemteljességi tétele bebizonyította, hogy a formalista filozófiának mindkét alapkövetelménye tarthatatlan: egyetlen, a matematika céljaira elég erõs kalkulus sem lehet szintaktikai értelemben teljes, és egyetlen ilyen kalkulus sem képes bizonyítani magáról az ellentmondásmentességet (vagyis nincs olyan matematikai elmélet, amelynek ellentmondásmentességét önmagában bizonyítani tudnánk, és így a többi elmélet ellentmondásmentességét erre vissza lehetne vezetni). Lakatos elismeri, hogy a matematikus-közösség jelentõs hányada még nem hajtott fejet e kudarc elõtt, és a Gödel-tételek negatív eredményeit a metalogikában, a bizonyításelméletben és hasonló területeken próbálja megkerülni, de szerinte az is belátható, hogy minden ilyen kísérlet, még ha bizonyos értelemben sikeresnek is tûnik (mint például az aritmetika ellentmondásmentességének a transzfinit indukcióra alapozott Gentzen-féle bizonyítása), menthetetlenül kilép az eredeti formalista program eulkleidészi keretei közül: az ellentmondásmentességgel és a teljességgel kapcsolatos intuíciónk alkalmatlan arra, hogy megalapozza a matematikát.

Nem marad más tehát hátra, mint hogy a további, kevésbé fontos történeti próbálkozások vizsgálata helyett immár levonjuk a konklúziót, hogy a matematika nem lehet eukleidészi jellegû. Vagyis a matematika tudománya egyrészt nem tévedhetetlen: nem tudtunk olyan mechanizmust mutatni, amely felelõs lehetne a tévedhetetlenségéért. Másrészt nem szigorúan bizonyító, ugyanis ehhez szükség lenne arra, hogy az axiómák a levezetett tételekhez képest feltétlen autoritással rendelkezzenek, ám a helyzet az, hogy sok esetben az axiómákat módosítjuk azzal a céllal, hogy a tételek “igazságát” biztosítani tudjuk (a viszony tehát megfordul – lásd cáfolás). Végül pedig a matematika nem is tisztán formális, hiszen a tisztán formális rendszerek nemcsak arra alkalmatlanok, hogy “szóljanak valamirõl”, hanem arra is, hogy megfeleljenek a velük szemben támasztott, intuitív formai elvárásainknak.

A matematiafilozófia összefonódása a matematikatörténettel
 

Azok az elképzelések tehát, amelyek arra törekedtek, hogy megállapítsák, milyennek kell lennie a matematikának, vagyis hogy elõírják a matematika számára, hogyan kell ideális esetben mûködnie, tarthatatlannak bizonyultak. A matematika filozófiájának inkább abból kell kiindulnia, hogy leírja a matematika valódi mûködését. Ehhez pedig a matematika történetéhez kell fordulnia: meg kell vizsgálnia, hogy valójában mi az a módszer, melyet a sikeres, a tudás gyarapodását szolgáló matematikai tevékenység követ. Részben ezt fejezi ki az a híres lakatosi tézis (Immanuel Kant egy filozófiai tételének parafrázisa), mellyel egyik leghíresebb tudományfilozófiai tanulmányát kezdi: “A tudományfilozófia a tudománytörténet nélkül üres, a tudománytörténet a tudományfilozófia nélkül vak.” ([4], 65. oldal)

A tézis elsõ részét tehát az eddigiek alapján könnyen magyarázhatjuk: Minden olyan tudományfilozófia, amelyik nem veszi figyelembe az általa vizsgált tudomány történetét, elvéti a saját tárgyát, hiszen nem ismeri meg annak valódi mûködését, természetét. (A tudományelméletek módszertanának e fontos követleményét fogalmazta meg Lakatossal egyidõben Thomas S. Kuhn, és kettejük hatására ma már kevés olyan tudományfilozófus alkot, aki ennek igazságát kétségbe vonná.) A tézis második fele azonban ennél jóval problematikusabb: azt állítja, hogy minden olyan történeti kutatás, amelyik nem egy filozófiai koncepció mentén halad, meddõ és értelmetlen. Hiszen a történész nem tiszta végcélként, minden további céltól mentesen fordul a tudomány történetéhez, hanem azzal a céllal, hogy választ kapjon erre a kérdésre: mi a tudomány? (És ezzel szoros összefüggésben: Mi a racionalitás?) Ez a filozófiai kérdés irányít minden történeti kutatást, az erre adott elõzetes válszunkat próbájuk alátámasztani minden olyan történeti adattal, melyet ezen “elõítéletünk” szerint választottunk ki. A történeti adatok halmaza ugyanis tökéletesen rendezetlen és áttekinthetetlenül terjedelmes, és elengedhetetlen, hogy rendelkezzünk olyan filozófiai elvárásokkal, melyek mentén a kusza adatokat egy történeti szállá rendezzük: ezt nevezi Lakatos racionális rekonstrukciónak.

Ez a fogalom aztán óriási vitákat keltett, és mind a mai napig heves tiltakozást vált ki a tudománytörténészek talán többségének részérõl. Mivel a kérdés részletes tárgyalása Lakatos általános tudománytörténeti írásainak vizsgálatát tenné szükségessé, és egy ilyen vizsgálat meghaladja tanulmányunk kereteit, szorítkozzunk most a híres lakatosi tézis elsõ részére, vagyis arra a követelményre, hogy minden tudományfilozófiai elméletnek a tudománytörténet alapos ismeretébõl kell kiindulnia.

Mit látunk akkor, amikor a matematika történetére tekintünk? A formalista matematikafilozófiával szembeni vita után rögtön szembetûnõ az a fontos tanulság, hogy a matematikai elméletek sosem formálisként adottak a matematikusok számára. A formális elméleteket mi, matematikusok hozzuk létre, méghozzá azzal a céllal, hogy precíz, fogalmilag rögzített keretbe foglaljunk egy informális elméletet. Mármost ez az informális elmélet az, ami elsõbbrendû a formális rendszerhez képest – ám ennek természetét igen nehéz megragadni, hiszen amíg nem kristályosodik ki a formális rendszer keretei között, addig ellenáll az egzakt fogalmi vizsgálatnak. A matematikai elméletek igazságának forrására vonatkozó kérdés tehát vizzsavezethetõ ezen informális fogalmi rendszerek igazságának kérdésére, ám erre a kérdésre Lakatos nem ad hagyományos, egyetlen mechanizmust kitüntetõ választ. Tapasztalatból kiinduló elvonatkoztatás, a platóni “örök igazságok” birodalmának intellektuális szemlélete, a matematikai objektumok fogalmi konstrukciójából adódó intuíció – Lakatos szerint mindez szerepet játszik az informális fogalomrendszer kialakításánál. A matematikafilozófiát azonban nem ez az ismeretelméleti probléma érdekli, hanem az, hogy hogyan jön létre a fogalmak rögzített rendszere, vagyis az a folyamat, amelyik a matematikai sejtéstõl a matematikai tudásig vezet.
 
 

A bizonyítások és cáfolatok módszere
 

A Bizonyítások és cáfolatok egy esettanulmány, egy olyan történeti folyamat “racionális rekonstrukciója”, amely Lakatos szerint kitûnõen alkalmas arra, hogy segítségével behatóan tanulmányozzuk, hogyan megy végbe a matematikai tudás gyarapodása. A vizsgált történeti folyamat a poliéderek elméletének 18-20. századi fejlõdése, és ezt segítségül hívva figyelemmel kísérhetjük egy informális intuíció fokozatos fogalmi letisztulását és végül formális elméletté merevülését. A folyamat fõ lépései a következõk:

1. Naiv sejtés. A matematikai kutatás mindig egy problémával kezdõdik (és megjegyzendõ, hogy mindig egy problémával is végzõdik). Ez a probléma egy összefüggés felismerése, amely megfogalmazható ugyan, de nem ágyazható olyan elméleti kontextusba, amelyben legitim és bevett módszerekkel bizonyíthatnánk. Ez tehát egyfajta “észrevétel”, amelynek forrása valamilyen intuíció, és semmiképpen sem egy deduktív matematika-képnek megfelelõen kapjuk. Esetünkben ez az észrevétel nem más, mint a (Descartes-)Euler-féle poliéder sejtés, vagyis az a meglátás (próbálgatások induktív igazolása alapján), hogy egy poliéderben a csúcsok száma plusz a lapok száma mínusz az élek száma egyenlõ kettõvel.

2. Bizonyítások és cáfolatok módszere. A soron következõ feladat az (ami egyben a matematika legfontosabb feladata), hogy létrehozzuk azt az elméletet, amelyben a fenti naiv sejtés tételként levezethetõ, vagyis rögzítsünk egy, a tárggyal kapcsolatos fogalmi keretet. Elõször is megpróbálunk adni egy “naiv bizonyítást” a “tételünkre”, másszóval “megmutatni”, “belátni”, hogy a tétel igaz. Esetünkben ez a Cauchy-féle “bizonyítást” jelenti, vagyis amikor a poliédereket gumilapokként fogjuk fel, és képzeletben az egyik élük mentén szétvágva és kiterítve õket, belátjuk a tétel igazságát. Ekkor azonban a matematikus-közösség számos tagja ki fogja használni a bizonyítás azon nyilvánvaló gyengeségét, hogy az a poliéderek mint “gumilapok” fogalmát használja ki, és könnyedén olyan ellenpéldákat hoznak, melyekre a fenti tétel nem igaz – ez a fázis tehát a kritika fázisa. Az ellenpéldákat nagyvonalúan két csoportra oszthatjuk: lokális és globális ellenpéldákra. A lokális ellenpéldát onnan ismerhetjük fel, hogy tulajdonképpen nem a tételünket cáfolja, hanem csupán egy kimondatlan lemmát, melyet tudtunk nélkül kihasználtunk a bizonyításnál – ekkor a kérdéses lemmát kicserélhetjük egy olyannal, amelyik már kizárja az ellenpéldát. A globális ellenpélda valóban a tételünket cáfolja, ám ekkor sem vetjük el a tételt és annak bizonyítását, hanem módisítjuk a fogalmainkat, vagyis felülbíráljuk azt, hogy mirõl szól a tétel és a bizonyítás (pl. mik azok a poliéderek). Ezáltal a bizonyítások, cáfolatok és bizonyítás-kritikák dialektikus kölcsönhatásán keresztül fokozatosan körvonalazódik egy fogalomrendszer, és ennek kapcsán egy “kutatási program” (a maga “kemény magjával” és “heurisztikájával” – lásd Lakatos tudományfilozófiai fogalomtárát [ 3] ), amely meghatározott keretet szab a matematikai tevékenység számára.

3. Deduktív elmélet. A kutatási program végül is létrehozza azt a (formális) elméletet, amelyben a kezdei naiv fogalmaink és bizonyításaink immár pontos jelentést kapnak. (Esetünkben létrejött az algebrai topológia axiomatikus rendszere.) Ekkor a tevékenység redukálódik a tiszta “rejtvényfejtésre” (Kuhn fogalmát veszi kölcsön Lakatos), és érdekes elméleti problémák már nem merülnek föl. A formalista filozófia számára egyedül ez a fázis érdekes – Lakatos számára ez a legkevésbé érdekes.

Érdekes megjegyezni, hogy Lakatos szerint ugyannek a feljõdési sémának a mûködése mutatható be a görög matematika kialakulásán is (volt tanárára, a híres matematikatörténészre, Szabó Árpádra hivatkozik ekkor), például a geometriában, Thálész naiv sejtéseitõl Eukleidész rendszerének létrejöttéig. És ami még érdekesebb, Lakatos ugyanezt a sémát látja érvényesnek a klasszikus mechanika születésére is: Kepler “naiv sejtéseitõl” (amelyek fizikai bizonyítására semmiféle komoly elmélet nem állt rendelkezésre a korban) egészen Newton “axiomatikus” megalapozásáig. Jelek utalnak arra, hogy élete utolsó néhány évében Lakatos sem módszerében, sem pedig tárgyában nem látta különbözõnek a matematikát és a természettudományokat – ezen nézetének explicit taglalása azonban sajnálatosan elmaradt.
 
 

Összefoglalás
 

Összefoglalásképpen szeretném segítségül hívni Lakatos azon vallomását (a második doktori disszertáció könszönetnyilvánításaiban), amelyben felsorolja, hogy matematikafilozófiájának kialakításában kik voltak rá a legnagyobb hatással:

1. Popper falszifikáció-elmélete – ebbõl megtanulhatta, hogy a tudományokban a bizonyítás fogalmát korántsem használhatjuk olyan naiv módon, mint azt sokáig gondolták, és hogy a cáfolatoknak legalább akkora szerepe van, mint a bizonyításnak.

2. Pólya György heurisztikája (Pólya A gondolkodás iskolája címû könyvét Latatos fordította magyarra) – ebbõl azt tanulhatta meg, hogy a matematika nem azonos formális elméleteknek egy csoportjával, hanem elválaszthatatlan az emberi tevékenységtõl, amellyel mi magunk hozzuk létre a matematikai vizsgálódás tárgyát.

3. Hegel dialektikája – ebbõl tanulta meg azt, hogy az egy adott tárggyal kapcsolatos filozófiai gondolkodás nem merülhet ki a fogalmi rögzítettség megragadásában, hanem ehelyett a fogalmi dinamikára kell fordítani a figyelmet, ugyanis így adhatunk számot ismereteink gyarapodásáról, a fejlõdésrõl. A matematika filozófiájának tehát a matematikai bizonyosság elméletébõl a matematikai feljõdés elméletévé kell elõlépnie.

Ajánlott irodalom

1. Lakatos legfontosabb felhasznált mûvei:

 

(1)	Bizonyítások és cáfolatok. Budapest, Typotex, 1998. (1963-64)
(2)	Lakatos Imre tudományfilozófiai írásai. Szerk: Miklós Tamás. Budapest, Atlantisz, 1997.   Ebben különösen:
(3)	“A kritika és a tudományos kutatási programok metodológiája”. 19-63. oldal (1967)
(4)	“A tudomány története és annak racionális rekonstrukciói”. 65-128. oldal (1970)
(5)	Mathematics, Science and Epistemology. Phil. Papers Vol. 2. Szerk. J. Worrall and G. Currie. CUP, 1980.   Ebben:
(6)	“Infinite regress and foundations of mathematics”. 3-23. oldal (1962)
(7)	“A renaissance of empiricism in the recent philosophy os mathematics?” 24-42. oldal (1965)
(8)	“What does a mathematical proof prove?” 61-69. oldal (1959-61)
(9)	“The method os analysis-synthesis. Part Two” 93-103. oldal (1973)

 

2. Néhány cikk Lakatos életérõl:

 

(10)	Condon, Lee: “Bûn és bûntelenség. Az ismeretlen Lakatos Imre”. Replika, 1998/29. 7-23. oldal
(11)	Kántor Sándorné Varga Tünde: “Lakatos Imre, a szintetikus modernizmus megalapítója” Debreceni Szemle, 1998. 273-283. oldal
(12)	Long, Jancis: “Lakatos Imre Magyarországon”. Magyar Filozófiai Szemle, 1999/1-2-3. 251-308. oldal
(13)	Mihályi Gábor: “Egy életkudarc története”. Replika, 1998/30. 183-188. oldal

 

3. Néhány cikk Lakatos munkásságáról:

 

(14)	Forrai Gábor: “Lakatos Imre tudományfilozófiája: vázlat”. Replika, 1996/23-24. 7-23. oldal
(15)	Kiss Olga: “Lakatos Imre matematikafilozófiája”. Replika, 1996/23-24. 25-38. oldal
(16)	Margitay Tihamér: “Racionalitás és objektivitás” Replika, 1996/23-24. 7-23. oldal