Difficulties of the standard interpretations of probability

We need to make a distinction between mathematical and realistic interpretations of probability. Mathematical interpretation means that the formal mathematical structure PROBABILITY THEORY is represented in ANOTHER FORMAL MATHEMATICAL STRUCTURE. Discussing the Bertrand-paradox, for example, we consider a representation of the probability-theoretic notions in geometrical terms. (The alleged ``paradox'' consists in the simple fact that we have a kind of freedom in constructing such a representation.)

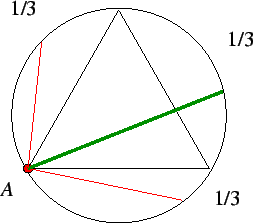
Problem: Given a circle. Find the probability that a chord chosen at random be longer than the side of an inscribed equilateral triangle.

Solution 1

Let us fix the point A and consider only the chords that emanate from this point. Then it becomes clear that 1/3 of the outcomes will result in a chord longer than the side of an equilateral triangle.

Solution 2

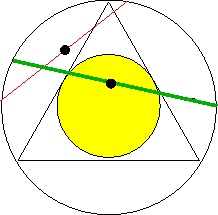
A chord is fully determined by its midpoint. Chords whose length exceeds the side of the triangle have their midpoints inside a smaller circle with radius $r=\frac{1}{2}R$. Hence, $p=\frac{\pi r^{2}}{\pi R^{2}}=\frac{1}{4}$.

It is also a mathematical representation when probabilities are represented by the limiting values of convergent relative-frequency-like infinite sequences, or when the (``subjective'') probabilities are represented in game-theoretic terms.

The mathematical interpretations do not raise difficulties at all. Our concern is, however, not a mathematical but a realistic interpretation. A realistic interpretation is nothing but the way in which we apply probability theory to the real world. The similarity between the mathematical and realistic interpretations is that in both cases we construct a representation of PROBABILITY THEORY in ANOTHER LANGUAGE. But, in case of a realistic interpretation this other language must be, in final analysis, translatable into empirical terms.

In this section I would like to briefly review the standard interpretations,³ and to illustrate that none of them is tenable, because none of them provides a sound definition of what probability is.