Physicalist Interpretation of Probability

As we have seen, although each of the standard interpretations can grasp something from our intuition about probability, none of them can provide an ultimate explanation, in empirical terms, of what probability is. How is it possible, on the other hand, that physics and other empirical sciences can apply the formal theory of probability, without perceiving anything from this unanswered fundamental question? In the second part of the paper I shall make an attempt to develop a new interpretation of probability, which perhaps can resolve this contradiction.

The key idea of my proposal is that probability is a concept which can be completely eliminated from the scientific discourse. This fact explains why the standard interpretations are unable to give a sound definition of probability, and also explains why empirical sciences can manage without such a definition.

Thesis 1 There is no such property of an event as its ``probability.'' What we call probability is always a physical quantity characterizing the state of affairs corresponding to the event in question.

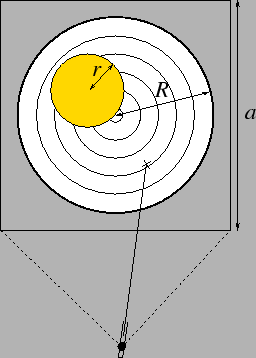
Consider the following example: A gun is hinged in such a way that it can shoot uniformly into a square of size $a\times a$ on the wall. Inside, there is a round target of radius $R$ and an air-balloon of radius $r$, in front of the target. What is the probability that the balloon bursts out (event $A$)? What is the probability that the shot hits the target (event $B$)? And what is the conditional probability of that the balloon bursts out, given that the bullet hits the target?

The physicist's standard answer to these questions is the following:

$$\begin{eqnarray*} p(A) & = & \frac{\pi r^{2}}{a^{2}}\\ p(B) & = & \frac{\pi R^{2}}{a^{2}}\\ p(A\vert B) & = & \frac{r^{2}}{R^{2}}\end{eqnarray*}$$

Let it remain in obscurity how the physicist arrives at these results. What is important is the fact that ``probability'' is expressed in terms of known, well-defined physical quantities, composing a dimensionless normalized measure on a space, the measurable subsets of which represent the outcome events in question. My suggestion is to give up the independent concept of ``probability'' with an overall context-independent meaning. In my view, this is what we must learn from the failure of the standard interpretations. The reason why none of these standard approaches can provide a sound meaning for the term ``probability'' is that there is no such a property of an event as its ``probability.'' That is, when we say that $p(A)=\frac{\pi r^{2}}{a^{2}}$, we do not mean that there is a known, well-defined quantity, $p(A)$, on the left hand side, which is, contingently, equal to $\frac{\pi r^{2}}{a^{2}}$. We just mean, that the measure $\mu(...)=\frac{\textrm{area of }...}{a^{2}}$ satisfies the Kolmogorov axioms and shows many other features we usually assign, intuitively, to probability.

In case of a completely different scenario, ``probability'' is identified with a dimensionless normalized measure composed by completely different physical quantities. So, the best what we can say about probability is the following:

Thesis 2 The term ``probability'' can be used only collectively: it means different dimensionless $\left[0,1\right]$-valued physical quantities, more precisely, different dimensionless normalized measures composed by different physical quantities in the different particular situations.

From the point of view of the everyday practice of sciences, the most important question is how probability is related to relative frequency. According to the above two Theses, it cannot be claimed, in general, that probability is equal to the limiting relative frequency, first of all because we do not know what probability is, in general. In the above example, we used the term ``probability'' for the quantity $\frac{\pi r^{2}}{a^{2}}$. In general, it has nothing to do with the relative frequency of event $A$. The value of $\frac{\pi r^{2}}{a^{2}}$ - although it is a well-defined number in each individual experiment, so, in this sense, ``probability'' is a meaningful notion for an individual event - can change during the sequential repetitions of the experiment (we can change the size of the balloon, for example), therefore there is no guarantee that the sequence of relative frequencies will converge to a limiting value.

But, in particular cases, if $\frac{\pi r^{2}}{a^{2}}$ is constant and the uniform distribution of the shots on the square is provided, the relative frequency of event $A$ is approximately, $o\left(\frac{1}{N}\right)$, equal to ``probability'' $\frac{\pi r^{2}}{a^{2}}$. (And this is not a probability-theoretic result but it is an elementary fact of kinematics.) In general,

Thesis 3 The physical quantity identified with ``probability'' is not the limiting value of relative frequency, and not even necessarily related to the notion of frequency. In some cases, the conditions of the sequential repetitions of a particular situation are such, however, that the probability (the corresponding physical quantity) is approximately equal to the relative frequency of the event in question.

Assume now, that we do not know the size of the balloon, therefore, we do not know the value of $\frac{\pi r^{2}}{a^{2}}$, i.e., the value of $p(A)$, but we know that it is constant, and we can also guarantee the uniform distribution of the shots. In this case, we can measure, $o\left(\frac{1}{N}\right)$, the ``probability'' $p(A)$, that is, $\frac{\pi r^{2}}{a^{2}}$, by measuring the relative frequency of $A$. That is,

Thesis 4 Sometimes we do not know the value of the physical quantity $X$, corresponding to the ``probability'' of an event $A$. In this case, if we are convinced about the relationship between $X$ and the relative frequency of $A$, we can measure $X$ by counting the relative frequency of $A$.

The physical quantity $\frac{\pi r^{2}}{a^{2}}$ exists and has a well-defined value, independently whether the laws of nature governing the shooting and the motion of the bullets are deterministic or not. Moreover, the relationship between $\frac{\pi r^{2}}{a^{2}}$ and the relative frequency of $A$ (if there is such a relationship at all) is not influenced by the deterministic or indeterministic character of the physical process in question. The relative frequency can be equal to $\frac{\pi r^{2}}{a^{2}}$ even if the uniform distribution of the shots are provided through a deterministic ergodic process, by the random number generator of a computer, for instance.

Similarly, nothing can influence the value of $\frac{\pi r^{2}}{a^{2}}$, which would be related to our knowledge about the details of the process. Similarly, if the condition of the uniform distribution of shots is satisfied, this value will be approximately equal to the relative frequency of $A$, independently of whether we know the direction of the subsequent shot, or not.

Finally, we have to emphasize that it is a matter of fact, whether the distribution of the shots is uniform or not. A priori we must not suppose that it is uniform, only because we have no information about how the directions of the consecutive shots are determined, and, on this basis, we have no reason to prefer one direction to the other.

So, our last three Theses are the following:

Thesis 5 The value of the physical quantity identified with ``probability'' is not influenced by the fact whether the process in question is indeterministic or not. And a priori there is no reason to suppose that this value can be only $0$ or $1$, only because the process is deterministic.

Thesis 6 The value of the physical quantity identified with ``probability'' is not influenced by the extent of our knowledge about the details of the process.

Thesis 7 Neither the value of the physical quantity identified with ``probability,'' nor the existence of the conditions under which this value and the relative frequency of the corresponding event are approximately equal can be knowable a priori.

Although the standard interpretations do not provide a coherent definition in empirical terms, they grasp many important aspects of our intuition of probability. The physical quantity like $\frac{\pi r^{2}}{a^{2}}$, in our example, seems to fit very well to these intuitive descriptions of probability:

1. In some sense it reflects the ratio of favorable cases to the number of equally possible cases.
2. Under suitable circumstances it is approximately equal to the relative frequency measured during the sequential repetitions of the experiment.
3. It is meaningful and has a definite value in each individual experiment.
4. In the example we investigated, the rate $\frac{\pi r^{2}}{a^{2}}$ expresses indeed the measure of the ``tendency'' of the whole system to behave in such a way that the balloon will burst out.

Of course, in the above context we could not deal with subjective probability. According to the physicalist account of mind, however, one can imagine a collection of physical quantities characterizing an agent's brain, which compose a dimensionless measure playing the same role in a typical betting scenario as the ``degree of belief.''

So, our physicalist account of probability grasps a big part of the intuition behind the standard approaches.