Termodinamikai folyamatok a kozmológiában

ELTE TTK szakdolgozat, csillagászat szak, 1999. tavaszi félév

Szerzõ: Kutrovátz Gábor
Témavezetõ: Martinás Katalin

Tartalom
 

1. Bevezetés

    1.1. Kiindulási problémák
    1.2. Rövid történeti áttekintés
    1.3. Az univerzum szokatlan helyzete

2. A termodinamika elméleti megalapozása

    2.1. Az axiómatikus út
    2.2. A Farkas-féle termodinamika
    2.3. A történelmi út

3. A modell

    3.1. A modell felépítése
    3.2. Entrópia a modellben
    3.3. Egy új fogalom: az extrópia
    3.4. Az univerzum extrópiája
    3.5. Termodinamikai kilátások
    3.6. A számítások eredményei
        3.6.1. Nyílt univerzum
        3.6.2. Zárt univerzum

4. A modellen túl

    4.1. A múlt
        4.1.1. A felfúvódási fázis termodinamikája
        4.1.2. Az anyagkomponensek kialakulása
        4.1.3. Lecsatolódások és entrópiaprodukció
    4.2. A jelen
        4.2.1. A reális helyzet
        4.2.2. Csillag és fotontér termikus kölcsönhatása
        4.2.3. Az RBH-modell: sugárzó fekete lyuk
        4.2.4. Az RBH-modell eredményei
        4.2.5. Az RBH-modell és a valódi fekete lyukak
    4.3. A jövõ
        4.3.1. Amit tudni vélünk
        4.3.2. A fekete lyukak elpárolgása
        4.3.3. Kétségek

Függelékek

    A. Függelék: A modell-világegyetem termodinamikája
    B. Függelék: A világegyetem extrópiájának kifejezése
    C. Függelék: Az univerzum sugarának fejlõdése
    D. Függelék: A sugárzási térbe ágyazott fekete lyuk termodinamikája

Források és hivatkozások


 

1. Bevezetés

1.1. Kiindulási problémák

Ha a világegyetemet egy izolált termodinamikai rendszernek tekintjük, akkor érvényes rá a termodinamika második fõtétele: a kozmosz a maximális entrópiájú állapotára törekszik. Ez az állapot a hõhalál. Ha ez bekövetkezik, akkor megszûnik a világegyetemben a munkavégzés, beáll a globális egyensúly, és jogosnak tûnik a feltételezés, hogy innentõl fogva a kozmosz nem hagyja el ezt az állapotát. Felmerül tehát a kérdés: miért nem állt be már ez az állapot a világegyetem eddigi története folyamán? És ha mégis beállt, akkor miért nem maradt fenn? Miért nem tapasztalunk globális egyensúlyt a világegyetemben? Másképpen szólva: honnan származik az az óriási mennyiségû szabadenergia, ami a világegyetemben végbemenõ folyamatok fenntartásához szükséges? És végül: vajon elkerülhetetlen-e, hogy a kozmosz elõbb vagy utóbb a hõhalál állapotába jusson?

Ezek olyan kérdések, melyekkel a modern kozmológiának éppúgy szembe kell néznie, mint a múlt század fizikájának, amikor a hõhalál gondolata egy paradoxon születéséhez vezetett. Ebben a dolgozatban annak járunk utána, hogy mai ismereteink alapján hogyan oldható fel ez a paradoxon.
 

1.2. Rövid történeti áttekintés

Az õsi teremtésmítoszok általában a rendet magyarázzák. Ezekben a teremtés folyamata olyan értelemben vetõdik fel, mint a káosz állapotának megszûntetése, a tapasztalatban megjelenõ rend létrehozása. A régi korok emberei arra keresték a választ, hogy miért van inkább a világon rend és szerkezet, mint a teljes káosz, mert úgy találták, hogy ez nem magától értedõdõ, tehát magyarázatra szorul.

A természetben érvényesülõ törvényszerûségek szisztematikus leírásának igénye elõször a görögöknél vetõdött fel, és ennek legszebb eredménye az arisztotelészi fizika rendszere. Ez a rendszer évszázadokra meghatározta a nyugati kultúra természettudományos világképét, ezért egy rövid pillantást kell vetnünk arra, hogyan vélekedett Arisztotelész fizikai tanításaiban a rend és káosz szerepérõl. Természetfilozófiája szerint minden test a “természetes helyére” törekszik, csakúgy, mint ahogy egy termodinamikai rendszer törekszik az egyensúlyi állapotába. Miért nem szûnik meg ezért a mozgás, miután minden test az õt megilletõ helyre ért? - kérdezte Arisztotelész, ahogyan mi is kérdezzük a hõhalál-elmélet árnyékában. A válasz: létezik egy mechanizmus, ami a testeket folyton kilöki a természetes helyükrõl, és ezen mechanizmus végsõ mûködtetõje egy isten-szerû lény, a Mozdulatlan Mozgató. A segítség tehát mintegy a világon kívülrõl érkezik, vagyis az arisztotelészi világ - a mi világegyetemünkkel ellentétben - termodinamikai értelemben nem zárt (bár anyagáram szempontjából igen).

Bár az arisztotelészi fizikát hevesen elutasító újkori mechanisztikus világképnek nem kellett szembenéznie ezzel a problémával, hiszen ha a világegyetemben az energia csak mechanikai energiaként létezik, akkor az energia-megmaradás tétele biztosítja a mozgás számára az örökkévalóságot, maga Newton mégis felelevenítette az arisztotelészi megoldást. Newton ugyanis tudta, hogy mechanikája nem érvényes egyöntetûen a természet minden jelenségére, és mivel tekintetbe vette a súrlódást is, feltételezte, hogy a mechanikai energia nem marad meg mindörökké. Ezért õ azt állította, hogy Isten, az “órásmester” idõrõl-idõre beavatkozik a világ fejlõdésébe, hogy pótolja az elveszett mechanikai energiát. Az õt követõ tudósok azonban inkább Leibniznek hittek a kérdésben, és azt gondolták, hogy mivel minden jelenség végsõ és igaz leírása mechanikai természetû, az energia nem veszik el, vagyis a világegyetem mozgásában örök.

Ez a nézet azonban válságba került a 19. század során, amikor a mechanika egyeduralmát más fizikai diszciplínák megerõsödése veszélyeztette. A termodinamika jelentõsége (többek között az ipari forradalom empirikus támogatásának köszönhetõen) óriási mértékben megnõtt, és ez új fogalmak és koncepciók megjelenését eredményezte a fizikában. 1865-ben Clausius megalkotta az entrópia fogalmát, és cikke végén az általa korábban már kimondott második fõtételt a világegyetem egészére a következõképpen vonatkoztatta:

“1. Az univerzum energiája állandó.

2. Az univerzum entrópiája egy maximumhoz tart.”

Ezzel pedig - úgy tûnik - elkerülhetetlenné vált a konklúzió: a világegyetem elõbb vagy utóbb eléri a maximális entrópiájú állapotát, és ezzel bekövetkezik az, amit a kortársak hõhalálnak neveztek el. Ebbõl pedig az következik, hogy a világegyetem nem létezhet öröktõl fogva, hiszen akkor már a hõhalál állapotában kellene lennie, ellentétben azzal, amit a mechanisztikus fizikai világkép állít. Íme a paradoxon.

A feloldás az 1930-as évekig váratott magára. Ekkor csillagászati megfigyelés (Hubble-törvény) és fizikai elmélet (általános relativitáselmélet) ötvözésének eredményeképpen megszületett az úgynevezett standard kozmológiai paradigma: a világegyetem története az õsrobbanásnak nevezett eseménnyel vette kezdetét, és azóta az univerzum folyamatosan tágul. Így nem szükségszerû azt gondolnunk, hogy a kozmosz valamikor a múltban elérte a hõhalál állapotát, hiszen lehetséges, hogy mindez egyszer majd csak a távoli jövõben fog bekövetkezni. Dolgozatunkban nem szólunk az olyan ma is létezõ, nem-standard kozmológiai elméletekrõl, mint amilyen például a folytonos teremtéssel kapcsolatos elképzelés, hiszen ezek (minthogy a világegyetemet anyagáramlás szempontjából is nyitottnak tekintik) a vizsgált problémánk tekintetében egészen más tárgyalásra szorulnak, mint amit a modern kozmológia általánosan elfogadott keretei között nyújtani tudunk. Éppen elég kérdéssel találjuk szemben magunkat ezen a szûkebb területen is, és ez jelzi, hogy a hõhalállal kapcsolatos paradoxon feloldása még egyáltalán nem vezetett a vonatkozó problémák általános megoldásához.

Vajon mennyire közel áll a világegyetem jelenlegi állapota a globális egyensúlyhoz, és ha elérjük, akkor mennyi idõ múlva érjük el a hõhalál állapotát? Hogyan tud számot adni a táguló univerzum elmélete a globális egyensúlytól való eltérésrõl, honnan származik a lokális fizikai rendszerek rendelkezésére álló szabadenergia? Mit értünk egy táguló világegyetem energiáján, illetve entrópiáján? Milyen értelemben tekinthetõ zártnak vagy izoláltnak egy táguló univerzum? Ezekkel és az ezekbõl következõ kérdésekkel kell megbirkóznunk ahhoz, hogy számot tudjunk adni a hõhalál-probléma jelenlegi helyzetérõl, és ezen keresztül a termodinamika szerepérõl a mai kozmológiában.
 

1.3. Az univerzum szokatlan helyzete

Ahhoz, hogy a világegyetemet mint termodinamikai rendszert vizsgálhassuk, tisztáznunk kell néhány olyan fogalmat, melyek a rendszer és környezete viszonyát segítenek jellemezni. Egy rendszer izolált, ha nincs anyag- és energiaáram a rendszer és környezete között. Egy zárt rendszer határa energetikailag átjárható, de anyagot õ sem cserélhet a környezetével. A kettõ közé helyezhetõ el az adiabatikusan szigetelt rendszer, ahol az energiacsere olyan értelemben nem megengedett, hogy hõközlés nem mehet végbe. Végül pedig a rendszer nyílt, ha mind energia, mind pedig anyag áramolhat a rendszer és környezete határán.

Nyilvánvaló, hogy ebben a felosztásban az univerzum izoláltnak adódik, hiszen anyag- és energiacsere elvileg sem lehetséges, ugyanis az univerzum környezetét fizikai rendszerként nem értelmezzük. (Persze a világegyetem fogalmának definiálása nem feladata sem ennek a dolgozatnak, sem a kozmológiának, de amennyiben elõzetesen elfogadjuk, hogy a világegyetem tartalmazza a fizikai elméleteink nyelvén leírható létezõk összességét, úgy a fizikai elméletben nyilván nem jelenhet meg az univerzum környezetének fogalma.) Ugyanakkor ez a szituáció olyan nehézségeket vet fel, amelyek a klasszikus termodinamikában, ahol minden rendszernek van környezete, nem jelenhetnek meg. Ilyen rendszereknél az izoláltság azt eredményezi, hogy a rendszer extenzív állapotjelzõi nem változhatnak. Ám a világegyetem tágul, vagyis térfogata nem konstans: ez a helyzet egy környezettel bíró rendszer esetén munkavégzést eredményezne, és a rendszer izolált voltát adiabatikusan szigeteltté szelídítené.

Mindebbõl már kitûnik, hogy a világegyetem termodinamikailag nehezen tárgyalható annyiban, amennyiben a termodinamika mindig a környezet viszonyában szemléli vizsgálata tárgyait. Ez a szokatlan helyzet pedig azt eredményezi, hogy a kozmológiai vizsgálódások során gyakran kell átlépnünk azon “tudományos intuíciónk” határait, amely a klasszikus rendszerek jól megszokott csoportjainak vizsgálatával alakult ki bennünk. Lássuk tehát, hogyan jelenik meg mindez a leírás során.


 

2. A termodinamika elméleti megalapozása

2.1. Az axiómatikus út

A termodinamika matematikailag szigorú axiomatikus felépítése az általánosan elfogadott nézet alapján Carathéodory-tól származik. Azt, hogy ennek vizsgálata szükséges a témánk szempontjából, az 1.3. alfejezetben felvetett problémák is mutatják. Néha felmerül a kétely, hogy az univerzum entrópiáját, minthogy környezet hiányában egy egyedülálló rendszerrõl van szó, nem is lehet definiálni. Hasonló problémák illusztrációjaként lássunk most egy gondolatmenetet, amely Lukács Béla megfontolásait követi.

Teljesen kézenfekvõnek tûnik annak feltételezése, hogy a termodinamikai folyamatok irreverzibilitása az entrópia globális növekedéséhez vezet. Ez az elgondolás, habár alátámasztja a józan ész és a fizikai intuíció, a termodinamika megszokott felépítésén kérhetõ számon, és alaposabb vizsgálatok során kiderül, hogy korántsem annyira magától értetõdõ, mint elsõ ránézésre gondolnánk.

A termodinamika szokásos elméletét követve tételezzük fel, hogy a világegyetem termodinamikai képét k darab Xi extenzív állapotjelzõ határozza meg. Ezek egyike legyen E, az energia. Ha egy infinitezimálisan kis elmozdulást teszünk az {Xi} fázistérben, akkor az energia dE megváltozása a következõképpen bontható fel:
 


dE = d W + d Q ,


ahol az elemi munka és az elemi hõáram nem teljes differenciáljai egy megfelelõ W, illetve Q függvénynek. Azt mondjuk, hogy a folyamatok irreverzibilitásáért a dQ tag felelõs (Clausius posztulátuma: két egyértelmûen meghatározott termodinamikai rendszer között spontán hõáram csak az egyik irányban lehetséges), ezért vizsgáljuk tovább ezt a tagot. Az elemi hõáram természetesen a következõképpen írható tovább:
 



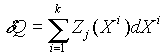
Ha adott a Zi függvények konkrét (az aktuális rendszerre jellemzõ) alakja, akkor az extenzív paraméterek k számától függõen a fenti kifejezés a következõ pfaffi kanonikus formákra hozható:
 

    k = 1 :     d Q = dQ(Xi)

    k = 2 :     d Q = T(Xi)dS(Xi)

    k = 3 :     d Q = dU(Xi) + T(Xi)dS(Xi)

    k = 4 :     d Q = H(Xi)dU(Xi) + T(Xi)dS(Xi)

    stb.

Amennyiben feltesszük egy abszolút hõmérsékletskála létezését, a k = 1 esetet (Lukács szerint) el kell vetnünk, és ekkor a k > 1 esetek jöhetnek csupán szóba. A termodinamika hagyományos felépítése a k = 2 teljesülésének feltételezésén alapul, és az adiabatikus tágulás vizsgálatánál mi is a dQ = TdS egyenlet érvényességébõl indultunk ki. Annál fogva is jogos ez a feltevés, hogy amint Landsberg kimutatta, k > 2 esetén a folyamatok irreverzibilitása nem vezet globális irreverzibilitáshoz, vagyis a fázistér bármely két pontja között mindkét irányban lehetséges az adiabatikus folyamattal történõ összeköttetés. Másszóval, az ilyen esetekben a másodfajú perpetuum mobile létezése lehetséges és megengedett, vagyis világegyetemet nem fenyegeti a hõhalál, hiszen nem létezik globális irreverzibilitás.

Ám ha mindez így is van, az említett szerzõ mégis úgy gondolja, hogy a termodinamika pfaffi formáinak vizsgálata nem ad valódi megoldást a problémára. Hiszen nem találkozunk a természetben másodfajú perpetuum mobile-kkel, és a
dQ = TdS törvény is maradéktalanul teljesülni látszik, tehát fel kell tételeznünk, hogy a Catathéodory-féle termodinamika továbbra is érvényes. Ez vagy azt jelenti, hogy a független extenzív paraméterek száma nem három, hanem csupán kettõ, vagy pedig azt, hogy bár a független paraméterek száma három (azért jogos ez a hozzáállás, mert a modellünket mi is ennek megfelelõen építjük fel), de valamilyen okból kifolyólag a dQ » TdS közelítés a szokásos körülmények között jól teljesül.

Ez utóbbi feltételezés természetesen semmit sem szól arról, hogy a termodinamika Caratheodory-féle formája érvényes volt-e a világegyetem igen korai fázisaiban, illetve hogy érvényes marad-e az igen távoli jövõben. Ha a második kérdésre a válasz nemleges is lehet, akkor hõhalál problémája nem vetõdik fel mint olyan kérdés, amit szükségszerûen meg kellene válaszolnunk - amennyiben a fenti gondolatmenetet elfogadjuk. Hogy a kérdésben dönteni tudjunk, lássuk most egy méltatlanul ismeretlen magyar matematikus és fizikus, Farkas Gyula termodinamika-felépítését, ami a tizennégy évvel a Carthéodory-féle elmélet elõtt került publikációra.
 

2.2. A Farkas-féle termodinamika

A következõ gondolatmenet talán nem egyszerû (igen sokáig észrevétlen is maradt), de tanulságai igen lényegesek a termodinamika szempontjából.

Határozzák meg egy rendszer állapotát a J , a, b, ... stb. paraméterek. Ha a folyamatok megfordíthatók, akkor az elemi hõ kifejezése a következõ formát ölti:
 


d Q = q dJ + A da + B db +... .


(Ennek kifejezése az elõzõ alfejezetben már szerepelt, ám most történeti okokból áttértünk Farkas jelöléseire.) Tételezzük fel, hogy a clausiusi posztulátum érvényes, azaz két rendszer között spontán (más változással nem járó) hõközlés csupán egy irányban lehetséges. Ebbõl következik a Farkas-lemma: adiabatikus úton egy test nem juttatható olyan állapotba, amibe puszta hõközléssel juttatható lenne. Ennek korolláriuma, hogy adiabatikus és reverzibilis folyamatban a hõmérsékletet teljesen meghatározza a többi állapotjelzõ értéke: J= J (a , b) . (Az állítás következése abból látszik, hogy az a- b sík egy tetszõleges pontja feletti adiabatikus reverzibilis folyamatot ábrázoló görbe csupán egyetlen hõmérsékletértéken haladhat át, lásd az
1. ábrát.)

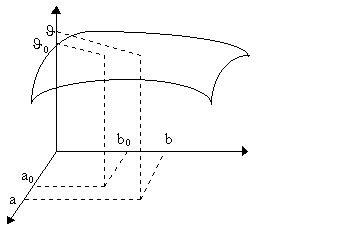1. ábra: A J-a-b állapottér

Ha egy termodinamikai rendszer állapota a J , a és b paraméterekkel van megadva, akkor bármely tetszõleges a0 és b0 pont az a–b síkon olyan, hogy felette bármely adiabata kiválaszt egy J0 hõmérsékletet. Az ezzel jellemzett adiabata egy olyan hõmérsékletfüggvény, amit J0 , a és b fog meghatározni. (Lásd a szöveget.)

Szorítkozzunk most az egyszerûség kedvéért arra az esetre, amikor J mellett csak a és b paramétereink vannak (1. ábra). Egy kiválasztott (a0 , b0) pont felett végtelen sok adiabatikus felület képzelhetõ el, melyeket az adott pontban felvett J0 hõmérséklet különböztet meg, ami viszont egyértelmûen kiválaszt egy J(a ,b) függvényt. Ezt a függvényt tehát
 


J = J (J0 , a , b)


 

alakban írhatjuk, amelynek teljes differenciálja a következõképpen néz ki:
 


,


 

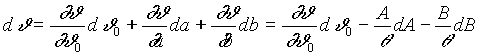mivel az a és b szerinti parciális deriváltakat állandó J0 mellett képeztük, és a dQ = 0 egyenletbõl kaptuk. Behelyettesítve dQ-nak azon kifejezését, melybõl kiindultunk, a következõ alakot kapjuk az elemi hõre:
 


.


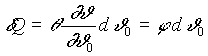Mivel a lemma miatt az adiabaták nem metszhetik egymást, a J0 függvény kifejezhetõ mint J0 = s(J, a , b) . jnem lehet zérus, hiszen Jfüggvénybõl kifejezhetõ J0 , vagyis ¶J/¶J0 sehol nem nulla. Ezért j -vel leosztva az alábbi eredményre jutunk:
 


,


 

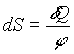vagyis az elemi hõközlés mennyiségét leoszthatjuk egy olyan j állapotfüggvénnyel, hogy az s állapotfüggvény teljes differenciálját kapjuk. Ezt másképpen úgy fejezzük ki, hogy a jfüggvény a hõközlés integráló-osztója.

Tegyük fel, hogy Y az s állapotfüggvénynek egy olyan állapotfüggvénye, hogy Ys szerinti teljes differenciálja nem nulla. Ekkor Ydifferenciálja a következõ:
 


,


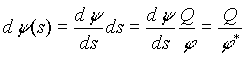ahol j* az a függvény, amit a j és a dY /ds hányadosaként kapunk. Ebbõl viszont az következik, hogy az integráló osztónkat tetszõlegesen választhatjuk meg, mert a potenciális jelöltek száma végtelen, melyeket az köt össze, hogy szintfelületeik az adiabaták.

Az s függvényt azonban egyértelmûbbé is tehetjük, ha megköveteljük, hogy additív legyen. Ekkor jelöljük S-sel az ilyen módon egy konstans szorzó erejéig meghatározott függvényt, és nevezzük entrópiának. Az additivitás feltétele kimondja, hogy az entrópia extenzív mennyiség. Ilyenkor mivel dS = dS1 + dS2, a hõ additivitása miatt:
 


dQ = dQ1 + dQ2 = f1 dS1 + f2 dS2 = f dS = f dS1 + f dS2 ,


vagyis f1 = f2 = f . Az f integráló osztónak tulajdonsága, hogy az egyensúly beálltával kiegyenlítõdik.

A továbbiakban a bizonyítást nem részletezzük, csupán a fõbb lépéseit közöljük. Elõször belátjuk, hogy egy két testbõl összetett rendszer esetén az s függvény az
 


s = s(J, s1 , s2 , b1 , b2)


alakban felírható. Azután bebizonyítjuk, hogy a rendszer s függvénye csak a részrendszerek s1 és s2 függvényeitõl függ: s = s(s1 , s2). Végül megmutatjuk, hogy a j integráló osztó egy szorzat alakjában írható fel:
 


j = f(J )Y (s) ,


Mivel tudjuk, hogy f integráló-osztó, és beláttuk, hogy ha j integráló-osztó, akkor j/Y(s) is az, levonhatjuk a következtetést, hogy létezik az abszolút hõmérsékleti skála, valamint létezik globális entrópia függvény.
 

2.3. A történelmi út

Hogyan illeszkedik a Farkas-bizonyítás a termodinamika történtébe, és mik a számunkra levonható következményei?

Az entrópia fogalmát Clausius vezette be, a róla elnevezett (és fentebb többször idézett) posztulátumból indítva el a termodinamika megalapozását. Clausius (negatívan) hivatkozik Zeuner-re, aki elõször keresett integráló osztót a hõ elemi kifejezéséhez, és azonosította azt az abszolút hõmérséklettel. Vagyis õ volt az elsõ, aki a hõmérsékletet sikeresen visszavezette más fogalmakra, nem pedig elsõdlegesen posztulált mennyiségként kezelte, bár még csupán a kétváltozós esetet vizsgálta. Clausius azonban a gondolatmenetet nem fogadta el, hiszen õ a hõmérsékletet (a többi termodinamikai fogalommal együtt) empirikus alapon kívánta megalapozni, és tekintélye elfordította a kutatók többségének figyelmét az integráló-osztó keresésének útjától.

A lineáris differenciál-kifejezések oszthatóságára vonatkozó matematikai eredmények Pfaff-tól származnak, aki bebizonyította, hogy a korábban felírt (róla elnevezett) kifejezéseknek kétváltozós esetben mindig van integrál-osztója, és Zeunert talán ez az eredmény térítette el a további vizsgálatoktól. A továbblépés Voigt munkáiban történt meg a múlt század végén, aki n változós esetben kereste az elemi hõ kifejezését. Amit azonban õ elfelejtett bizonyítani, azt Farkas pótolta: igazolni kellett az adiabatikus felületek létezését. Bár Voigt még elismerte Farkas eredményét, Carathéodory már nem említi Farkast, bár igen valószínû, hogy ismerte munkásságának vonatkozó részét.

A két véglet a termodinamika felépítésében tehát egyfelõl a clausiusi tradíció, amely a tapasztalati fogalmakra építi a hõtan megalapozását, másfelõl a pfaffi irány, amely tisztán matematikai megfontolásokkal kíván eredményre jutni. A történelmi utat követve az entrópia létezése nem különösebben szorul igazolásra, hiszen a hõ elemi kifejezésébõl indulunk ki, vagyis rögtön a kétváltozós esetben járunk, amikor az integráló-osztó létezése nem kétséges. Az axiomatikus-deduktív elméletben azonban kérdésessé válik, hogy a történelmi út kívánt eredménye szükségszerûen következik-e, hiszen itt mindennemû empirikus megszorítás nélkül szeretnénk eljutni a célhoz, ami a priori úton nem megy. A Farkas-féle bizonyítás a két tradíciót ötvözi: a szigorú matematikai elmélet keretein belül halad, ám kiindulópontja a tapasztalat szolgáltatta clausiusi posztulátum.

A továbbiak során a 2.1. alfejezetben ismertetett gondolatmenettõl el kívánjuk határolni magunkat. Nem azért, mintha a logikai menete hibás lenne, hanem inkább azért, mert véleményünk szerint helyénvalóbb egy fordított logikai utat követni. Számunkra nem az a kérdés, hogy a számos matematikai lehetõség közül miért pont a “legkedvezõbb” valósul meg, hanem inkább az, hogy a legegyszerûbb empirikus posztulátumokból kiindulva milyen eredményre juthatunk a matematikai elmélet alapján. Márpedig ha a clausiusi posztulátum igaz, akkor létezik globális hõmérséklet- és entrópia-függvény, és ezt mindaddig nyugodt lelkiismerettel feltételezhetjük, amíg valaki ellenpéldát nem talál.


 

3. A modell

3.1. A modell felépítése

A következõ egyszerû modellben az univerzumot mint rendszert három extenzív állapotjelzõ segítségével jellemezzük:

1.) Térfogat, illetve az ennek egyértelmûen megfeleltethetõ skálafaktor, “az univerzum sugara” (R). Ennek idõbeli viselkedését (homogén és izotróp kozmosz esetén) az egyik Einstein-egyenlet írja le:
 


,


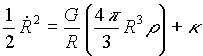ahol G a gravitációs konstans, r a homogén anyag- és energiasûrûség, k pedig egy integrációs állandó, amelynek értéke azt dönti el, hogy a világegyetem – nem termodinamikailag, hanem metrikusan – nyílt-e (k³ 0), avagy zárt (k< 0).

2.) Energia. A rendszert izoláltnak tekintjük, vagyis feltételezzük, hogy a tágulás adiabatikus. Ekkor érvényes rá a termodinamika elsõ fõtétele:

,


ahol E az univerzum belsõ energiája, P a nyomása és V a térfogata. (Megjegyzendõ, hogy az univerzum teljes energiája természetesen állandó, hiszen mint láttuk, izolált rendszernek tekinthetjük. A belsõ energia viszont a gravitációs energia rovására csökken, ami szintén nehezen értelmezhetõ klasszikus fogalmak segítségével.)

3.) Részecskeszám. Ebben a modellben ezt anyagkomponensenként állandónak tételezzük fel, és egyelõre nem vizsgáljuk a különbözõ anyagfajták egymásba történõ átalakulásának lehetõségét.
 

3.2. Entrópia a modellben

Ha a világegyetem egyfajta (homogén eloszlású) anyagot tartalmazna, a fenti egyenletek alapján entrópiája állandó lenne, hiszen adiabatikus tágulásnál dQ = 0 , vagyis dS = dQ/T = 0 . (Nem-homogén anyag esetén az entrópiát a belsõ folyamatok növelik.) Hogyan befolyásolja ezt az eredményt, ha többfajta anyag is jelen van? Tekintsük kétfajta anyagkomponens párhuzamos jelenlétét: az egyik egy homogén és izotróp feketetestsugárzás, a másik egy szintén homogén és izotróp atomos hidrogéngáz.

Ha csak sugárzás töltené be a teret, a világegyetem entrópiája a következõképpen alakulna:

,


ahol A egy állandó, Ts a sugárzás hõmérséklete, R a skálafaktor. Adiabatikus tágulás esetén ez azt jelenti, hogy a
 


Ts·R = konstans


érvényessége biztosítaná az entrópia állandó értékét, vagyis a Ts hõmérséklet a skálafaktorral lenne fordítottan arányos. Ha viszont csak (egyatomos) ideális gáz létezne, annak entrópiáját így számíthatnánk:
 


,


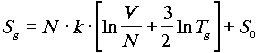ahol N a részecskeszám, k a Boltzmann-állandó, Tg a gáz hõmérséklete, S0 pedig egy integrációs állandó. Itt az adiabatikus folyamatra fennáll, hogy , hiszen a modellben a részecskeszám állandó, vagyis  , azaz = konstans. Ekkor tehát a gáz hõmérséklete a skálafaktor négyzetével fordítottan arányos:
 


= konstans.


Ezek szerint a táguló világegyetemben a sugárzás és a gáz különbözõ hûlési törvényeket követ, és ha mindkét komponens jelenlétét megengedjük, akkor kölcsönhatásukon keresztül egy hõmérséklet-kiegyenlítõdési folyamat lép fel: a komponensek tágulása külön-külön nem adiabatikus. Nézzük meg, mit jelent ez az entrópia szempontjából.

Legyen a lassabban hûlõ sugárzásról a gyorsabban hûlõ gázra folyó hõáram dQ. Ekkor a gázra fennáll, hogy 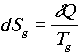 , illetve a sugárzásra igaz, hogy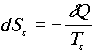 . A világegyetem összentrópiájának differenciálja:


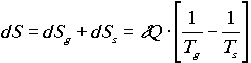
Ha feltesszük, hogy kezdetben Ts(0) = Tg(0), akkor az eltérõ hûlési ráták miatt késõbb mindig igaz, hogy Ts > Tg . Ez a kép csak akkor sérülhet, ha a világegyetem egy esetleges összehúzódási fázisban van, ugyanis (ahogy ezt a konkrét számítások ki fogják mutatni) ilyenkor a gáz hômérséklete a sugárzási hômérséklet fölé emelkedhet. Természetesen azt várjuk, hogy az entrópiaprodukció ilyenkor se legyen negatív, és ezt igazolja is a következô megfontolás: ebben az esetben a hôáram fordított irányban folyik, vagyis dS fenti kifejezésében a hômérsékleti tagok fordított elôjellel szerepelnek, és így az entrópia megváltozása továbbra is pozitív. Összességében tehát elmondható, hogy a világegyetem fejlôdése során mindig igaz, hogy dS > 0. (Az entrópia idôfüggésének precíz meghatározása az A. Függelékben található.)
 

3.3. Egy új fogalom: az extrópia

A további vizsgálatainkat szemléletesebbé és érdekesebbé tehetjük egy új termodinamikai állapotjelzõ, az extrópia bevezetésével, ami talán a modell által sugallt konklúziók megragadásának is hatékony eszköze lehet. Az extrópia egy entrópia-jellegû mennyiség, amely annak kifejezésére szolgál, hogy milyen távol van a rendszer egyensúlyi állapotától: mekkora annak az entrópiaprodukciónak a mértéke, amely abból származna, ha a rendszer jelenlegi állapotából a környezettel való egyensúlyra jutna. Így tehát az extrópia a rendszer és a környezet egyensúlyi összentrópiájának és ezek aktuális összentrópiájának különbsége:
 



Látható, hogy az extrópia egy olyan fogalom, amely fizikai szemléletünk követelményeit jól kielégíti. Egyfelõl segít kézzelfoghatóvá tenni számunkra, hogy egy termodinamikai rendszer mennyi lehetõséget rejt magában az energia-felhasználás, munkavégzés szempontjából, másfelõl annak kifejezésére is szolgál, hogy egy rendszer egyáltalán milyen mértékben különül el a környezetétõl. Minél közelebb van az extrópia értéke a zérushoz, annál inkább beleolvad a rendszer a környezetébe, ha pedig ez az érték eléri a nullát, a rendszer és környezete energetikailag megkülönböztethetetlenekké válnak. Emellett az extrópia, mivel az egyensúlyi állapothoz képest vett negatív entrópiaként számítjuk, a rendezettség mértéke is lehet, amennyiben a teljes rendezetlenséghez hasonlítjuk.
 

3.4. Az univerzum extrópiája

Mivel a világegyetem környezetét fizikailag nem értelmezzük, ezért az univerzum extrópiájának kiszámításánál csakis az õ entrópiáját kell figyelembe vennünk:

Ez azt jelenti, hogy amikor az univerzum extrópiája nullává válik, akkor nem a környezettével kerül egyensúlyba, hanem maga az univerzum éri el egyensúlyi állapotát. Az elôzôekben láttuk azt, hogy egyszerû modellünkben az univerzum aktuális entrópiája folyton nõ, ezért az extrópia kifejezésében a második tag PU csökkentésére törekszik. Változik azonban a világegyetem “egyensúlyi” entrópiája is, vagyis az a mennyiség, amely az egymással termikus egyensúlyban levõ, homogén eloszlású komponensek összentrópiája lenne az adott extenzív paraméterek mellett. A változás oka ezen paraméterek egyikének, a térfogatnak a növekedése. Vajon hogyan viszonyul az egyensúlyi entrópia változása az aktuális entrópia változásához, vagyis hogyan viselkedik az univerzum extrópiája?

Az univerzum extrópiáját egy adott állapotban úgy is felfoghatjuk, mint annak az entrópiának a mennyiségét, amit az univerzum akkor termelne, ha az adott állapotból termikus egyensúlyra jutna rögzített extenzív paraméterek mellett. Ennek egy (jó közelítéssel élô) kiszámítását találhatjuk meg a B. Függelékben. A számítások eredménye azt mutatja, hogy az extrópia csupán a komponensek hômérsékletétôl és hôkapacitásától függ, amit el is várunk egy olyan mennyiségtôl, ami a termikus egyensúlytól való távolságot méri. Az extrópia tehát akkor maximális, ha a komponensek hômérsékletkülönbségének abszolút értéke maximális, vagyis az extrópia problémája, és ezen keresztül a hôhalál problémája is, visszavezethetô a hômérsékletek meghatározásának kérdésére.
 

3.5. Termodinamikai kilátások

Hogy a tágulás vajon örökké fog-e tartani, az ma még eldöntetlen kérdés. Várható, hogy mivel egy nyílt világegyetemben mindkét anyagkomponens hômérséklete a nullához tart, az extrópia is tetszôlegesen kicsivé válik kellôen hosszú idô elteltével, vagyis ha a hôhalál paradoxonát fel is tudja oldani a táguló világegyetem, a hôhalál fenyegetésétôl nem tud megszabadulni. Ugyanis ha a komponensek közötti kölcsönhatás mértéke nem zérus (tehát van értelme termodinamikai folyamatokról beszélni), akkor a hômérséklet-kiegyenlítôdési folyamat véges idô elteltével eljuttatja a hômérsékletükkel aszimptotikusan egymáshoz közeledô komponenseket az egyensúlyi állapotba.

Ezen az eredményen az sem sokat segítene, ha a tágulás következtében a komponensek közötti kölcsönhatás elôbb nullává válhatna, minthogy elérkeznének a közös egyensúlyi hômérsékletre (a modell ezt nem teszi lehetôvé, mert a kölcsönhatás paraméterét konstansnak veszi). Ekkor ugyanis egy másfajta hôhalál köszöntene be, a globális termikus izoláció, és ez ugyanúgy befagyasztana a világegyetemben minden folyamatot, mint a globális termikus egyensúly. A hôhalál fogalma tehát annyiban ma is teljesen helytálló fogalom, amennyiben azt sugallja, hogy mivel a véges világegyetemben csupán véges munkavégzésre van lehetôség (termodinamika második fôtétele), a világegyetem termodinamikailag nem mûködhet végtelen hosszú ideig.

Valószínû, hogy egy zárt világegyetemben a hôhalál állapotának bekövetkezése attól függ, hogy az anyagkomponensek közötti kölcsönhatás milyen gyorsan közelíti a világegyetemet a termikus egyensúlyhoz, vagyis hogy beáll-e a globális egyensúly a végsô összeroppanás elôtt. Ha az univerzum hosszú ideig létezik, akkor kitágulhat olyan mértékben, hogy a komponensek hômérséklete fizikai szempontból gyakorlatilag nullává váljék, és ekkor beáll a hôhalál egy “közbülsô” szakasza. Ez azonban nem végleges állapot, ugyanis elôbb-utóbb meg kell szûnnie, ahogy a következô megfontolások mutatják.

Ha a tágulási szakaszt összehúzódási fázis követi, akkor ott az anyagkomponensek újra felmelegednek, ám ezt nem a lehûlésükre szimmetrikusan teszik, hiszen köztük kölcsönhatást tételezünk fel, melynek iránya az összehúzódási szakasz kezdetekor természetesen nem fordul meg. Az univerzum tágulása tehát nem reverzibilis: mivel a kölcsönhatás a tágulási hûlésbôl származó hômérsékletkülönbség ellen dolgozott, összehúzódáskor a termikus egyensúlyt a világegyetem elõbb eléri, mint hogy a sugara visszaesne arra a kezdeti értékre, amelynél az egyensúly a tágulás során megbomlott (modellünkben ez az érték zérus). Ám ez az egyensúly egyáltalán nem egyezik meg a hôhalál állapotával, hiszen csak egy pillanatig áll fenn: a hûlési törvényekre szimmetrikus felmelegedési törvényeknek megfelelôen az addig hidegebb komponens ekkor melegebbé válik, és a hômérsékletek különbsége rohamosan nôni fog. A világegyetem ezen utolsó szakasza tehát még tartogathat meglepetéseket.

Vizsgáljuk meg végül, hogy hogyan tükrözôdnek a fenti megfontolások a modell konkrét számításainak eredményeiben.
 

3.6. A számítások eredményei

3.6.1. Nyílt univerzum

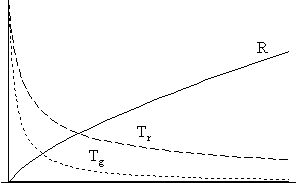
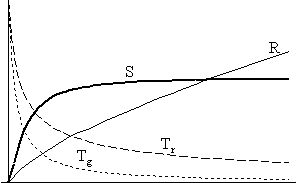
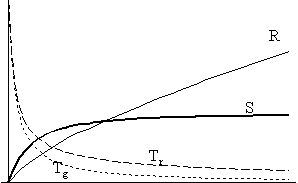
Az alábbi ábrasorozat a világegyetem különbözô fizikai jellemzôinek változását mutatja az idô függvényében, amennyiben a világegyetem nyílt, vagyis az Einstein-egyenletben k>0. A bal oldali ábrákon a következô mennyiségek idôbeli függvénye szerepel:
 

    R: az “univerzum sugara” (vékony folytonos vonal);

    Tr: a sugárzási komponens hômérséklete (ritkán szaggatott vonal);

    Tg: a gázkomponens hômérséklete (sûrûn szaggatott vonal);

    S: az univerzum entrópiája (vastag folytonos vonal).
 

A fenti mennyiségek meghatározására szolgáló differenciálegyenlet-rendszer, illetve annak levezetése az A. Függelékben található.

A jobb oldali ábrák a világegyetem entrópikus jellemzôinek változását mutatják, úgy mint:
 

    S: az entrópia (vastag folytonos vonal);

    P : az extrópia (szaggatott vonal);

    Smax: az adott skálafaktor mellett a maximálisan elérhetô entrópia:

    Smax = S + P (vékony folytonos vonal).
 

Az extrópia meghatározásának levezetése a B. Függelékben szerepel.

Az egymás alatt látható ábrák abban térnek el egymástól, hogy az egyenletek megoldásakor különbözô numerikus értékeket választottam annak a paraméternek, ami a két komponens közötti kölcsönhatás erôsségét jellemzi. Az 2/a ábrákon ezen paraméter értéke nulla, vagyis a komponensek között nincs kölcsönhatás, majd az ábrákon lefelé haladva a paraméter értéke egyre nô. Egyéb kezdôfeltételben az ábrák által bemutatott modell-univerzumok nem térnek el egymástól.
 
 

2. ábrák: A termodinamikai paraméterek változása nyílt univerzum esetén

(Az ábrák magyarázatát lásd a szövegben.)
 
 

2/a/I.                                                     2/a/II.

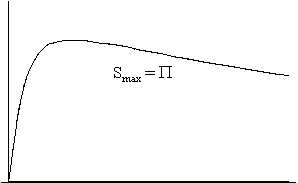t                 t
                                S = 0                                                                                         S = 0

2/b/I.                                                     2/b/II.

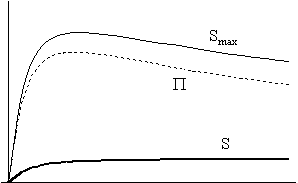t                 t

2/c/I.                                                       2/c/II.

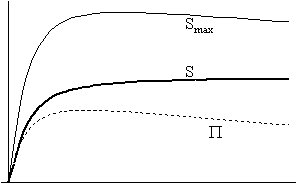t                 t

2/d/I.                                                         2/d/II.

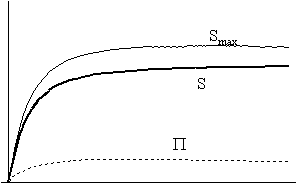t                 t

2/e/I.                                                     2/e/II.

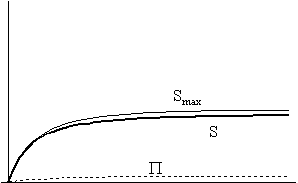t                 t
 
 

Nézzük meg most az eredményeket lépésenként!

A 2/a/II. ábrán jól látható, hogy amennyiben a komponensek között nincs kölcsönhatás, úgy - hôáram híján - az entrópia természetesen konstansan zérus. Ekkor a Tr sugárzási hômérséklet az R-1 függvény szerint csökken, és mivel a skálafaktor az idôvel megközelítôleg lineárisan nô (eltekintve a korai szakasztól), jó közelítéssel azt mondhatjuk, hogy a Tr ~ t-1 arányosság fennáll. Ugyanilyen megfontolások alapján élhetünk azzal a közelítéssel, hogy Tg ~ t-2 . A 2/a/II. ábráról leolvasható, hogy mivel az entrópia mindenütt nulla, az extrópia értéke minden pontban megegyezik a maximális entrópia értékével. Az extrópia-függvény alakja viszont némi magyarázatra szorul. A függvény ott veszi fel a maximumát, ahol a két komponens hômérsékletkülönbségének abszolút értéke maximális. Ez egészen magától értetôdô, hiszen az univerzum termikus egyensúlytól mért távolsága ekkor a legnagyobb. Ezek után az extrópia a hômérsékletkülönbséggel együtt csökken, és ennek megfelelôen tart a nullához.

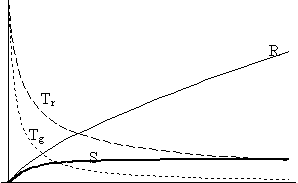
A 2/b/I. ábra azt az esetet mutatja, amikor a komponensek között már van kölcsönhatás, bár még csak csekély. Látható, hogy ekkor megjelenik az entrópia folyton növekvô függvénye, és a 2/b/II. ábrának megfelelôen ez ahhoz vezet, hogy az extrópia és a maximálisan elérhetô entrópia függvényei szétválnak. Ez a jelenség fokozódik a kölcsönhatási paraméter további növelésével: a 2/c/I. ábrán az entrópia keletkezése nagyobb mértékû, és a kölcsönhatás erôsödésének következményeként már szemmel látható, hogy a komponensek hômérsékletei az eddigi ábrákhoz képest közelebb vannak egymáshoz. Megjegyzendô, hogy ez utóbbi effektus azzal jár, hogy egyrészt csökkenni fog az extrópia (ami akkor maximális, amikor a hômérsékletkülönbség is az, vagyis a kiindulási ábrákkal bemutatott esetben), másrészt pedig a hômérsékletkülönbség csak késôbb éri el maximumát, és így az extrópia-függvény maximuma is jobbra tolódik, ahogy az a 2/c/II. ábráról leolvasható.

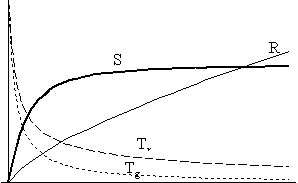
A kölcsönhatási paraméter tetszôleges további növelése azonban nem jár együtt az entrópia-függvény vég nélküli növekedésével. Ábrasorozatunkon az entrópia a 2/d ábrákon éri el maximális futását, a 2/e ábrákon azonban újra kisebb értékeket vesz fel. Ennek oka az, hogy bár a kölcsönhatás erôsségének növekedése eddig dominánsan befolyásolta az entrópia alakulását, mostantól nagyobb szerepet játszik a hômérsékletkülönbség csökkenése, ami viszont az entrópiaprodukció mértékének leeséséért felelôs. Eddigre már az extrópia igencsak lecsökken, ahogy az a 2/e/II. ábrán látszik, vagyis az entrópia-függvény fokozatosan hozzásimul a maximális entrópiát leíró görbéhez: a heves kölcsönhatás arra az eredményre vezet, hogy az univerzum minden pillanatban közel van az egyensúlyi állapotához. Ha a kölcsönhatási paramétert igen nagynak (gyakorlatilag végtelennek) választjuk, akkor a két komponens hômérséklete minden idôpontban azonos lesz, és mind az entrópia, mind az extrópia konstansan zérus függvényt vesz fel: a világegyetem fejlôdése során mindvégig a termikus egyensúly állapotában marad.
 

3.6.2. Zárt univerzum

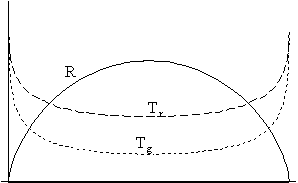
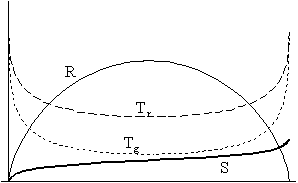
Az alább látható ábrasorozat teljesen hasonló a nyílt univerzum esetén bemutatott sorozathoz. Ugyanazoknak a fizikai mennyiségeknek az idôbeli alakulását ábrázoltuk mind a jobb, mind a bal oldali ábrákon, mint az elôzô esetben, és ugyanúgy öt különbözô modell-világegyetemet mutatunk be olyan sorrendben, hogy az A. Függelékben található egyenletrendszer megoldásakor egyre nagyobb numerikus értéket tulajdonítunk a komponensek kölcsönhatását jellemzô paraméternek.
 

3. ábra: A termodinamikai paraméterek változása zárt univerzum esetén

(Az ábra magyarázatát lásd a szövegben.)
 

3/a/I.                                                     3/a/II.

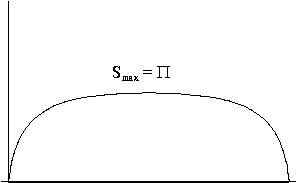                 t t
                        S = 0                                                                     S = 0

3/b/I.                                                     3/b/II.

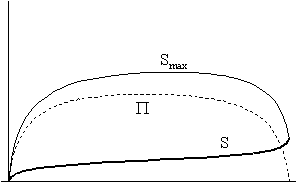                 t t

3/c/I.                                                     3/c/II.

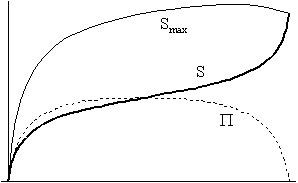                 t t

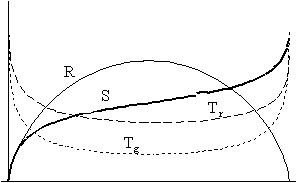
3/d/I.                                                     3/d/II.

                 t t

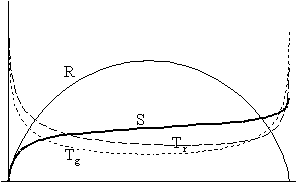
3/e/I.                                                      3/e/II.

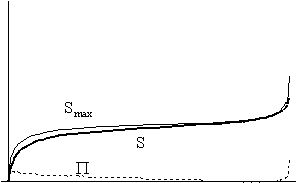                 t t
 
 

Érdemes ebben az esetben is részletesen megvizsgálnunk a kapott eredményeket.

Amikor a kölcsönhatási paraméter értéke nulla (3/a/I.), a hômérséklet-görbék teljesen szimmetrikusan futnak a kezdeti értéküktôl az azonos nagyságú végsô értékükig. Az entrópia-függvény természetesen minden pontban a zérus értéket veszi fel.

Ezekbôl következôen az extrópia-görbe is szimmetrikus (3/a/II.), ám az a tény, hogy az univerzum maximális méretével egyidôben veszi fel maximumát, a paraméterek megválasztásának esetleges következménye. Ha ugyanis az univerzum “kevésbé zárt” lenne, vagyis az Einstein-egyenletben a k paraméter értéke az általam választottnál kisebb volna, akkor hosszabb ideig élne, és a hômérsékletek különbségének abszolút értéke csökkenni kezdene azelôtt, hogy a skálafaktor elérné maximális értékét. Ekkor az extrópia-függvénynek két maximuma volna, egy a tágulási szakaszban fellépô maximális hômérsékletkülönbség idején, egy pedig - erre szimmetrikusan - az összehúzódási fázis maximális hômérsékletkülönbségének idején. Ez a helyzet látható a 4. ábrán. Mivel azonban a többi mennyiség vizsgálata szempontjából kedvezôbb, ha a kezdeti és végsô stádiumok, ahol a változások hevesebbek, nagyobb hangsúlyt kapnak az ábrákon, a jelenségek általános vizsgálatához azt az esetet választottuk, amikor ennek a viszonylag “unalmas” középsô stádiumnak nincs ideje megjelenni.
 
 

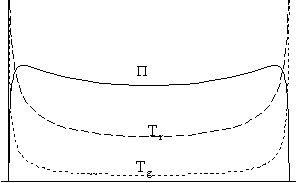    4. ábra: Az extrópia zárt univerzumban

Az extrópia akkor maximális, amikor a két komponens hõmérséklete leginkább eltér. Mivel az univerzum maximális méreténél a hõmérsékletkülönbségnek lokális minimuma lehet, ezért az extrópia is helyi minimumot vehet fel ezen a ponton.
 

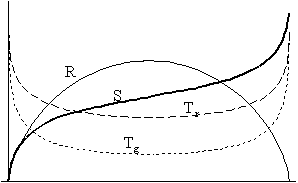
Térjünk vissza az ábrasorozatunkhoz! A 3/b. ábrákon a nemzérus kölcsönhatás következtében megjelenik a nemzérus entrópia-görbe, majd a kölcsönhatás erôsödtével magasabb értékeket vesz fel (3/c). Megjegyzendô, hogy a 3/c/II. ábrán már világosan látszik, miszerint az extrópia futása nem szimmetrikus, hiszen a hômérsékletek kiegyenlítôdésére irányuló folyamat következtében a maximális hômérsékletkülönbség állapota egyre korábbra tolódik el, és távolodik attól a ponttól, ahol az univerzum eléri maximális méretét.

Elsô ránézésre talán nem sok különbség látszik a 3/c/I. és a 3/d/I. ábrák között, legfeljebb csupán annyi, hogy az entrópia-görbe egy csöppet visszaesett, vagyis itt is szerephez jut az az effektus, ami az egyre erôsebb kölcsönhatás entrópia-növelô hatását az egyre kisebb hômérsékletkülönbséggel, és így egyre kevésbé heves folyamatokkal ellensúlyozza. Ám az igencsak lényegi eltérés a 3/c/II. és a 3/d/II. ábrák összehasonlításakor érhetô tetten: a maximális entrópiát ábrázoló görbe az utóbbi esetben nem érintkezik az aktuális entrópia görbéjével a végpontjukban, vagyis (ahogy az látszik is) az extrópia végsô értéke a második esetben nem nulla. Sôt, a görbérôl az is leolvasható, hogy az extrópia-függvény valamivel a futása vége elôtt felveszi a zérus értéket, majd hirtelen megugrik. A talán váratlan jelenség oka, ahogy azt korábban már elôrejeleztük, abban keresendô, hogy az eddigieknél erôsebb kölcsönhatásnak sikerült elérnie, hogy a két komponens hômérséklete még az ún. W-pont (végsô szingularitás) elôtt szemmel láthatólag kiegyenlítôdjön: az extrópia-függvény természetesen ekkor veszi fel a nulla értéket. Ettôl kezdve a gázkomponens természeténél fogva gyorsabban melegszik (Tg ~ R-2), mint a sugárzási komponens (Tr ~ R-1), és mivel az egyre gyorsabban változó skálafaktor mellett a kölcsönhatás nem képes a pillanatnyi egyensúlyt visszaállítani, a két hômérséklet-görbe ezen a ponton metszi egymást.

Ez a jelenség tisztán kivehetô a 3/e/I. ábrán, ahol a hômérséklet-görbék mindvégig erôsen megközelítik egymást, majd pedig egy ponton “helyet cserélnek”. Az extrópia ekkor már mindenhol alacsony értéket vesz fel (3/e/II.), és a korábbi ábrákon megjelenô maximuma (vagyis a táguláskor jelentkezô maximális hômérsékletkülönbség idôpontja) igen koránra tolódik el. Növekszik azonban az újonnan megjelent, az W- pontban elért maximum értéke, és már itt is nagyobb a korábbi maximuménál. Bár eddig is tisztában voltunk azzal, hogy egy “eléggé” zárt univerzumban nem fenyeget a hôhalál veszélye, most a modell-univerzumunk szempontjából levonhatunk egy talán kevéssé lényeges, de annál érdekesebb konklúziót: Akármilyen hosszú (de elég hosszú, vagyis nem túl rövid) ideig létezik egy zárt univerzum, és ebbôl következôen akármilyen hosszú ideig is tart az esetlegesen fellépô hôhalál “közbülsô” állapota, az összehúzódási fázis végén a világegyetem feltámad termodinamikai “poraiból”, és a legvégsô pillanatban messzebbre távolodik a termikus egyensúlytól, mint egész korábbi történetében bármikor.


 

4. A modellen túl

Modellünkben adottnak tekintettünk kétfajta anyagot: a fotongázt és az atomos hidrogént. Ez talán jó közelítésnek tûnhet a világegyetem mai állapotának jellemzésére, de további kérdéseket vet fel a múlttal, a jelennel és a jövõvel kapcsolatban. Vajon csak ezt a két komponenst kell-e figyelembe vennünk, vagy vannak ezeken kívül mások is, amik számottevõ szerepet játszanak a kozmosz irreverzibilis tágulásában? Meddig tételezhetjük fel jogosan e két komponens jelenlétét, amikor gondolatban visszafelé haladunk az univerzum korai fázisai felé, vagy amikor vizsgálatainkat az egyre távolabbi jövõre szeretnénk vonatkoztatni? Ezek a kérdések szükségessé teszik, hogy egy rövid pillantást vessünk a világegyetem múltjára, jelenére és jövõjére a mai fizikai elméletek alapján.
 

4.1. A múlt

4.1.1. A felfúvódási fázis termodinamikája

Közismert, hogy a világegyetem inflációs szakaszában a nyomásnak negatívnak kellett lennie ahhoz, hogy a modell magyarázattal szolgálhasson azokra a problémákra, amelyek megoldására született. A jelenség kimutatásához tekintsük az univerzum kezdeti állapotát, vagyis azt az állapotot, amikor a végesen kis V térfogatú világegyetemben a vákuum a teljesen szimmetrikus állapotban található. A felfúvódási modell szerint a vákuum energetikailag legkedvezõbb (zérus) állapota, a “valódi” vákuum különbözik ettõl a nemzérus energiájú “hamis” vákuumtól (5. ábra). Ezért a vákuum hamis állapota metastabil, amibõl bármilyen kis fluktuáció kibillenti a korai univerzumot.
 
 

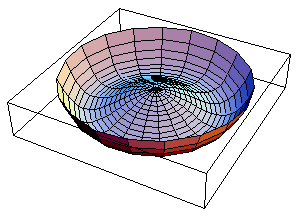        5. ábra: A vákuumpotenciál

Egy kétdimenziósra redukált vákuumpotenciál szemléltetõ ábrája. Az ábra szerint a vákuum szimmetrikus alapállapota nem egyezik meg a legalacsonyabb energiájú állapotával. Ha a vízszintes síkban lefektethetõ tengelyekre az ún. Higgs-vektorokat vesszük fel, akkor legalább az egyik Higgs-tér mentén a szimmetria megbomlik, amikor a vákuum a legalacsonyabb energiaszintre kerül.
 

Gondolatban rögzítsük egy “kis idõre” az univerzum sugarát. Tegyük fel, hogy a tér valamely kicsiny v térfogatában a vákuum energetikai alapállapotba kerül. Mivel ez az állapot kedvezõbb, a régió terjedni kezd, vagyis térfogata nõ a hamis vákuum térfogatának rovására. Hõközlést most nem tételezünk fel, ezért a hamis vákuum energiaváltozása a dE = - dW képlettel írható le, ahol dW a hamis vákuum által végzett munka: dW = pdV. Tudjuk, hogy a hamis vákuum energiaváltozása negatív, hiszen mennyisége a folyamatban csökken, tehát munkavégzése pozitív. Ám mivel a térfogata is csökken, a pozitív munkavégzést csak úgy kapjuk meg, ha feltételezzük, hogy a hamis vákuum nyomása negatív (míg a valódi vákuum nyomása feltételezésünk szerint nulla).

Mivel a hamis vákuum energiasûrûsége , másfelõl viszont láttuk, hogy dE = - pdV, adódik, hogy u = - p. Ha feltételezzük, hogy az univerzum ezen korai fázisában is érvényesek a tágulásra vonatkozó Einstein-egyenletek, akkor a
C. Függelékben levezetett


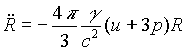
egyenletet összevetve fenti eredményünkkel azt láthatjuk, hogy amíg hamis vákuumot tartalmazó régió teljesen el nem tûnik, addig a tágulás üteme egyre növekszik, méghozzá exponenciális mértékben. A negatív nyomás “felfújja” a világegyetemet: ezt a jelenséget nevezzük felfúvódásnak vagy inflációnak.

Az inflációs világegyetem-modell sok olyan problémát megoldott, amivel a standard kozmológiai paradigmának szembe kellett néznie (horizont-probléma, laposság-probléma, simaság-probléma, monopólus-probléma), ezért megszületése után rövidesen uralkodó pozícióra jutott a kozmológiai elméletek körében. Néhány szerzõ azonban a fenti sikert úgy magyarázza, hogy az elméletnek egy ad hoc és abszurd feltételezésre volt szüksége az említett problémák megoldásához: a negatív abszolút nyomás bevezetésére. Érdemes néhány szót szólni arról, hogy ez a feltételezés valóban annyira elképesztõ-e, mint amennyire elsõ ránézésre tûnik: a természetben valóban elképzelhetetlen-e negatív nyomású állapot megjelenése.

Amikor gázokat vizsgálunk, a nyomást a gázrészecskék és a gázt tartalmazó edény fala közti ütközésekbõl származó erõhatásként értelmezzük. Ilyenkor természetes, hogy a nyomás pozitív, és csak akkor válhat nullává, ha az edény falait a végtelenbe távolítjuk. Ha ebbõl a képbõl indulunk ki, negatív abszolút nyomást nem tudunk elképzelni. Azonban ez az értelmezés olyannyira nem általános, hogy csak gázok vizsgálatára alkalmazható. Hiszen érdemes a nyomást egy háromdimenziós tenzorként tekinteni:
 
 

P =  ,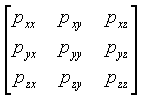

ahol gázok esetén a diagonális elemek megegyeznek, a többi tag pedig nulla. A nyomás skaláris értéke :

Tr(P) ,


 


ami természetesen nem szükségszerûen pozitív vagy nulla.

A negatív abszolút nyomás kimutatására ismert legegyszerûbb módszerek az edénybe zárt folyadékok hûtésével kapcsolatos kísérletek. Ha egy folyadékot hûtünk, térfogatának csökkennie kellene, ám ha a folyadék nedvesítõ, akkor az edény falához tapad, és nem tud összehúzódni. Ekkor a folyadék nem “nyomja”, hanem “húzza” az edény falát, vagyis nyomása negatív. Ha Huygens korai próbálkozásaitól eltekintünk, ilyen jellegû szisztematikus kísérleteket elõször Maurice Berthelot végzett az 1850-es években a negatív nyomás vizsgálatára; ma úgy tudjuk, hogy víz esetén kb. - 150 MPa nyomást lehet a fenti módszerrel elérni. Nagy szerepet játszanak negatív nyomású állapotok hidrodinamikai örvényekben, valamint számos élõ szervezetben, mint például a fákban és a polipokban. Minthogy az erre vonatkozó ismereteink még napról napra bõvülnek, a biztosan levonható konklúziót állapítsuk meg annyiban, hogy a természet egyáltalán nem szûkölködik negatív abszolút nyomású állapotokban. (A helyzet nagyban hasonlít ahhoz, ahogyan a negatív abszolút hõmérséklet fogalma egyre nagyobb teret nyer a fizikai elméletekben.) Végeredményben tehát a kozmosz inflációs fázisában megjelenõ negatív abszolút nyomás feltételezése talán sokkal természetesebb elképzelés, mint a kozmológiai modellek számos más eleme.
 

4.1.2. Az anyagkomponensek kialakulása

“Kezdetben” (az Õsrobbanás pillanatához tetszõlegesen közel) a kvantumvákuum teljesen relativisztikus, nulla nyugalmi tömegû, végtelen hatótávolságú részecskékbõl állt, melyek eltérõ ei töltésekkel csatolódtak a F= 0 paraméterû szimmetrikus vákuumtérhez. Azonban ahogy láthattuk, a vákuum alapállapota F0 nemzérus paraméterrel jellemezhetõ, így a tér látens energiája felszabadult, és a vákuum fázistranszformáción ment keresztül, amelynek következtében a részecskék eiF 0 = mic2 nyugalmi energiára tettek szert, valamint az általuk közvetített kölcsönhatások hatótávolsága bi = h/mic értékre csökkent. Ez az átmenet tehát a tér felfúvódását okozta, amely ennek következtében megközelítõleg euklídeszivé simult.

A gyors tágulás azt eredményezte, hogy a tér hõmérséklete rohamosan csökkenni kezdett. Míg eleinte a kvark-antikvark párok és a fotonok közti q + q- « X « 2g átmenet egy X-részecskén keresztül teljesen szimmetrikusan mehetett végbe, amikor a hõmérséklet a mxc2/k érték alá esett, a termikus egyensúly megbomlott, és az X-részecskék instabilakká váltak. Ám mivel a felfúvódás során a vákuumnak el kellett hagynia a teljesen szimmetrikus (ám energetikailag nem a legkedvezõbb) egyensúlyi állapotát, a világegyetem szimmetriája sérült, és így valamennyivel több kvark keletkezett, mint antikvark.

Késõbb a keletkezett kvarkok és antikvarkok annihilálódtak, ám a fennmaradó kvarktöbblet (az eredeti mennyiség mintegy százmilliomod része) fõként protonokká és neutronokká állt össze. A neutronok ugyan instabil részecskék, ám igen lassú bomlásuk (kb. tíz perces felezési idõ) lehetõvé tette, hogy a szabad protonok befogják õket, és a magkölcsönhatás segítségével stabilakká váljanak. Az így kialakult atommagok protonjai már csak virtuális X-részecskéken keresztül, alagúteffektus segítségével sugározhatnak szét, ám mivel az (mx - mp) c2 potenciálgát viszonylag magas (a protonok felezési idejét 1032 évre becsülik), a barionos anyag még sokáig jelen lesz a világegyetemben.

A kvark-antikvark párok annihilációja után a világegyetemet a termikus egyensúlyban lévõ fotonok és leptonok dominálták. Ám a tágulás során az anyag sûrûsége az univerzum növekvõ sugarával köbösen csökkent, így a ritkuló anyagban az ütközések közti szabad úthossz egy idõ után meghaladta az univerzum mértét. A gyenge kölcsönhatásban résztvevõ semleges részecskék, a neutrínók lecsatolódtak a töltött részecskékrõl és a fotonoktól, bár a töltés hiánya miatt ugyanazt a hûlési törvényt követték, mint a fotonok. Ám amikor a hõmérséklet az elektronok (és pozitronok) tömege által meghatározott mec2/k érték alá süllyedt, az elektron-pozitron párok többsége szétsugárzódott. Az így felszabadult energia a fotongáz hõmérsékletét növelte, vagyis a neutrínógáz és a fotontér közti termikus egyensúly megbomlott.

Összefoglalásképpen lássunk egy táblázatot a világegyetem történetének kezdeti fázisairól:
 

1. Táblázat: A korai univerzum fázisai
 
t [s]
T [K]
A domináns anyag
< 10-10 > 1015 Gyenge mértékbozonok: W± , Z0 : minden azonnal annihilál
10-10 - 10-4 1015 - 1012 Kvark-gluon plazma: a kvarkbezárás lehetségessé válik
10-4 - 10-2 1012 - 1011 Hadronok: az aszimmetria miatt a szétsugárzás utáni többlet
10-2 - 10 1011 - 109 Leptonok: itt is többlet marad a szétsugárzás után
10 - 1011 109 - 104 Fotonok: a semleges atomokról a sugárzás lecsatolódik
> 1011 < 104 Galaxisok: a barionos anyag gravitációs szervezõdésekbe áll

4.1.3. Lecsatolódások és entrópiaprodukció

A világegyetem tágulásából következõ hõmérsékletcsökkenés néha más úton is hozzájárul az összentrópia növekedéséhez, mint a komponensek kölcsönhatása. Amikor a tágulás során a hõmérséklet annyira lecsökken, hogy valamely részecske lecsatolódik a kezdeti, energetikailag teljesen homogén állapotról, az univerzum anyagkomponenseinek száma nõ. Nézzük meg egy nagyon egyszerû modellen, hogyan változnak ilyenkor az univerzum entrópikus jellemzõi, és milyen hatással van a lecsatolódás az egyensúly alakulására.

Tételezzük fel, hogy a világegyetemet (vagy annak egy termodinamikai alrendszerét) egy adott t1 idõpillanatban egy homogén eloszlású, egyetlen részecskefajtából álló gáz tölti ki. Ezután fázisátmenet következik, aminek eredményeképpen a t2 > t1 idõpillanatban már két, energetikailag eltérõ állapottal jellemezhetõ anyagkomponens lesz jelen. A statisztikus mechanika szerint egy rendszer entrópiája a következõképpen fejezhetõ ki:
 


S = - k å pi ln pi ,


ahol k a Boltzmann-állandó, pi pedig az i-edik mikroállapot bekövetkezésének valószínûsége. A modell-világegyetem entrópiája tehát a lecsatolódás elõtt zérus, ugyanis csak egyetlen mikroállapot elérhetõ a részecskék számára, aminek bekövetkezési valószínûsége nyilvánvalóan p1 = 1 , vagyis
 


S1 = - k 1ln 1 = 0 .


 


Másszóval az univerzum a teljes rendezettség állapotában van.

Tegyük fel, hogy a lecsatolódás után kétfajta részecske népesíti be a világegyetemet, ahol a különbözõ részecskék elõfordulásának relatív gyakorisága 1:2. Ha a sebesség és a hely szerinti eloszlást az egyszerûség kedvéért továbbra sem különböztetjük meg, akkor a t2 idõpontban az összentrópia így alakul:
 


S2 = - k (1/3 ln 1/3 + 2/3 ln 2/3) » 0,64 k .


Tehát a modell-világegyetem összentrópiája megnõtt, ám ez a növekedés korántsem jelenti azt, hogy a rendszer közelebb került volna az egyensúlyi állapotához, hiszen eleve egyensúlyban volt: inkább arról van szó, hogy a lecsatolódás elôtti és utáni világegyetem két különbözô termodinamikai rendszert alkot. (Ezért is nevezzük néha a lecsatolódásokat fázisátalakulásnak.)

Lássuk tehát most az extrópia megváltozását! Emlékezzünk, hogy az extrópia a rendszer maximális entrópiájú állapotától mért távolságát jelenti az entrópia-skálán. Feltéve, hogy n különbözõ mikroállapot jelenléte esetén a maximális entrópia az
 


Smax = k ln n


alakban írható, a modell-világegyetemünk maximális entrópiája t1 idõpontban zérus lesz, hiszen n = 1 , és ln 1 = 0 ; t2 idõpontban viszont n = 2 , vagyis

S2max = k ln 2 » 0,69 k .


Vagyis a lecsatolódás során az entrópia aktuális értéke kevésbé nõtt meg, mint az egyensúlyi állapotot jellemzõ, maximálisan elérhetõ entrópia, másszóval a világegyetem extrópiája növekedett, az univerzum távolabb került az egyensúlytól.

Természetesen egyszerû algebrai megfontolásokkal belátható, hogy a fenti eredmény általánosítható a tetszõleges n komponensû állapotból kiinduló és tetszõleges m (> n) komponensû állapotba érkezõ fázisátalakulásra. Az entrópia mindig nõni fog, az extrópia pedig általában nõni, és sohasem csökkenni (bár ha a komponensek relatív gyakorisága 1:1, akkor értéke változatlan maradhat). Ezért a kezdeti tágulás mellett egy újabb folyamatot találtunk, ami egyszerre növeli az entrópiát és az extrópiát: a fázisátalakulások különösen hatékony eszközei mind az entrópiatermelésnek, mind pedig a globális termikus egyensúly (másszóval hõhalál) állapotától való eltávolodásnak
 

4.2. A jelen

4.2.1. A reális helyzet

A mai univerzum legfontosabb anyagkomponensei, ahogy a 4.1.2. alfejezetben beszámoltunk róla, a fotongáz, a neutrínógáz és a barionos anyag. A fotonanyagot és a neutrínóanyagot homogén és izotróp eloszlású gázoknak foghatjuk fel, melyek tehát önmagukkal egyensúlyban vannak. Mivel nincs közöttük kölcsönhatás, a világegyetem növekvõ irreverzibilitásához nem járul hozzá az a tény, hogy a két gáz - a fotontér korai, e-- e+ annihilációkból származó felfûtése miatt -nincs egymással termikus egyensúlyban. (Ráadásul a köztük levõ hõmérsékletkülönbség is mindvégig csökken, hiszen mindketten az R-1-es hûlési törvényt követik.) A neutrínógáz a barionos anyaggal sem áll számottevõ kölcsönhatásban, így bár az eltérõ hûlési rátájuk eleinte lehetõvé tenné a világegyetem összentrópiájának növelését, hõközlés híján tágulásuk egymáshoz képest adiabatikus. Úgy tûnhet tehát, hogy modellünk megközelítõleg helyesnek tekinthetõ, hiszen a globális irreverzibilitásért leginkább a fotongáz és a barionos anyag kölcsönhatása felelõs.

Ám a helyzet valójában sokkal összetettebb annál, mint azt a modell alapján várni lehetne. Hiszen a világegyetemben található fotongáz, illetve barionos anyag nem homogén eloszlású (bár nagyléptéken annak tekinthetõ), és az anyag-komponensek nincsenek önmagukkal termikus egyensúlyban. A nemegyensúlyiság oka csillagászati természetû: a hideg, nemrelativisztikus barionos anyag gravitációs eredetû inhomogenitásokba szervezõdik, ezáltal sajátos nyomás- és hõmérséklet-viszonyokat hozva létre. Az összesûrûsödött gáz a részecskék felszabaduló potenciális energiáját sugárzás formájában tudja leadni, és így fûti a fotonteret. Ráadásul kellõ mértékû sûrûsödés esetén beindulnak a magreakciók, melyek a hõmérsékletet tovább növelik, és a kisugárzás intenzitását is megsokszorozzák. Valójában tehát nem a gáznál lassabban hûlõ fotontér hõközlése a legszámottevõbb entrópiatermelõ folyamat a világegyetem jelenlegi fázisában, hanem sokkal inkább az, hogy a felmelegedett barionos anyag fûti a nála jóval hidegebb fotonteret.

Lássunk erre egy példát!
 

4.2.2. Csillag és fotontér termikus kölcsönhatása

A csillagok termodinamikai szempontból igen különleges objektumok, ugyanis hõkapacitásuk negatív. A különös jelenség már akkor megmutatkozik, amikor a kialakulóban levõ csillag összehúzódik. Ekkor a részecskék potenciális energiája kinetikus energiává alakul át, amelytõl a protocsillag sugárzás formájában szabadulna meg. Ám a sugárzás következtében a belsõ nyomás lecsökken, és a protocsillag méginkább összehúzódik, aminek hatására tovább sugározza energiáját. Ez az öngerjesztõ folyamat azt eredményezi, hogy a gáz hõmérséklete egyre magasabb lesz, mialatt folyamatosan hõt sugároz ki, és ez a hõtan nyelvén negatív hõkapacitást jelent.

Ez a jelenség addig áll fenn, amíg az anyag összehúzódásra képes, hiszen a közölt hõ forrása a gravitációs tér által végzett munka. Amikor a kontrakció leáll (a részecskék közti valamilyen taszító kölcsönhatásnak köszönhetõen), akkor az összetömörült anyag már zavartalanul leadhatja az energiáját, de csakis abban az esetben, ha tömege nem haladja meg a termonukleáris fúzió beindulásához szükséges kritikus tömeget. Mert ha meghaladja, akkor a keletkezett csillag belsõ energiatermelése, és ezen keresztül sugárzása (tömegének függvényében) még hosszú ideig biztosított. Miután a csillag egyensúlya beállt, a fúzió következtében tovább folytatja (immár lassú) összehúzódását, hiszen magja kondenzálódik, és ezért a folyamatos sugárzás ellenére felszíne tovább forrósodik. A csillag hõkapacitása továbbra is negatív, bár a hõ forrása immár a magban lezajló termonukleáris reakció. Vizsgáljuk meg most ezen hõleadásnak a kozmikus fotontérre kifejtett hatását!
 

4.2.3. Az RBH-modell: sugárzó fekete lyuk

A csillagot modellezzük az egyszerûség kedvéért egy (nemforgó) fekete lyukkal, amelyik természetesen sugárzást bocsát ki. Hawking és Beckenstein munkáját követve feltesszük, hogy egy fekete lyuk entrópiája (természetes mértékegység-rendszerben számolva) a lyuk keresztmetszetének és a gravitációs állandónak a hányadosa:

,


 


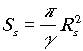ahol g a gravitációs állandó, és Rs a Schwarzschild-sugár: Rs = 2gMs , ha Ms a fekete lyuk tömege. Vagyis az entrópia így írható tovább:
 


Ss = 4pMs2g.


 


Mivel a munkavégzést a hõközléshez képest elhanyagoljuk, ezért úgy vesszük, hogy dEs = Ts dSs , és minthogy Es = Ms (hiszen a fénysebesség: c = 1), a lyuk hõmérsékletére a következõ összefüggés adódik:
 


.


 


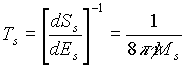Ennek alapján látszik, hogy a fekete lyuk hõkapacitása a várakozásunknak megfelelõen negatív, ugyanis
 


.


 


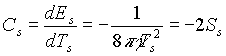A Stefann-Boltzmann törvény szerint a fekete lyuk egységnyi felületének luminozitása a hõmérséklet negyedik hatványával arányos: L = aTs4 , ahol a egy konstans, így a lyuk teljes luminozitása:
 


Ls = (4pRs2)( aTs4) = a* Ts2

(a konstansokkal nem törõdve).

Helyezzük most gondolatban ezt a csillagot modellezõ fekete lyukat sugárzási térbe. Ekkor az általa sugárzott hõáram a következõképpen írható:
 


dQ = a* Ts -2(Ts4 - Tr4) ,


ahol Tr a sugárzási tér hõmérséklete. Ekkor a teljes entrópiaváltozás a következõ alakot ölti:

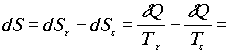
= a* Ts 3Tr (Ts4 - Tr4) (Ts - Tr) > 0 .


Természetesen itt egy megjegyzés kívánkozik arról, hogy a fenti eredmény, vagyis hogy a fekete lyuk nem stabil, és bármilyen kis fluktuáció kibillenti az egyensúlyából, mennyiben alkalmazható a valódi csillagokra. A fekete lyuk esetén maga az entrópia-mátrix negatív, míg a csillagok esetén a negatív hõkapacitású állapot csak egy bizonyos sugárzási és összehúzódási folyamatot jellemez. Ha a csillag energiatermelése leáll, illetve amikor beindul a magasabb rendszámú elemek égetése, megszûnik a lassú összehúzódás, és a hõkapacitás pozitívvá válik. A modellünk tehát a csillagoknak csupán egy bizonyos (ám igen jelentõs) életszakaszára alkalmazható.
 

4.2.4. Az RBH-modell eredményei

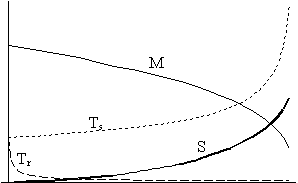
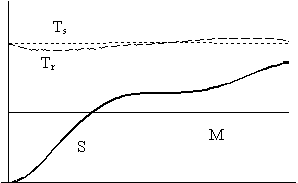
A 6. ábra mutatja be a termodinamikai paraméterek változását nyílt (6/a.), illetve zárt (6/b.) világegyetem esetén. Az ábrázolt fizikai mennyiségek a következôk:

    M: a csillag, avagy a fekete lyuk tömege (vékony folytonos vonal),

    Ts: a fekete lyuk hômérséklete (sûrûn szaggatott vonal),

    Tr: a sugárzási tér hômérséklete (ritkán szaggatott vonal),

    S: a csillag-fotontér rendszer entrópiája (vastag folytonos vonal).
 

Az elôzô alfejezetet kiegészítô számítások, vagyis a szükséges egyenletek levezetései a D. Függelékben találhatók.
 

5. ábra: Sugárzási tér és belé ágyazott fekete lyuk nyílt és zárt univerzumban

5/a.: Nyitott univerzum                                 5/b.: Zárt univerzum

                
                                                                        t                                                                                                 t
 

Az számítások azzal az egyszerûsítéssel élnek, hogy feltevésünk szerint a fekete lyukkal modellezett csillag már jelen van gyakorlatilag a világegyetem keletkezésének idôpontjában (a szimuláció kiindulási pillanatában), és hogy hômérséklete ekkor megegyezik a sugárzási komponens hômérsékletével. Ez a feltevés valószínûleg nem sokat von le a modell kvalitatív értékébôl, viszont alaposan megkönnyíti a szimulációt, ha minden görbe minden pontban definiált.

Nyílt univerzum esetén, ahogy azt a korábbi megfontolások alapján vártuk is, az a hômérsékletek közötti, eltávolító hatású visszacsatolás figyelhetô meg, ami a csillag negatív hôkapacitásának eredményeképpen lép fel. A sugárzási hômérséklet valamivel kevésbé meredeken csökken, mint amit a rá jellemzô R-1-es összefüggés határozna meg, hiszen a csillag folyamatosan hôt közöl a fotontérrel. Viszont ennek megfelelôen a csillag egyre inkább felforrósodik, és eközben egyre csökken a tömege. Ám mivel a kölcsönhatás erôssége a hômérsékletek különbségének abszolút értékével együtt nô, az effektus önmagát fokozza, amíg végül a csillag minden energiáját kisugározza, és hômérséklete felszökik igen magasra, gyakorlatilag a végtelenbe. Ez az eredmény szemmel követhetô a 6/a. ábrán látható Ts görbe futása alapján. Eközben az entrópia is egyre nô, ugyanis az igen gyorsan fokozódó hômérsékletkülönbség hatását nem tudja az egyre lassabban táguló univerzum anyagsûrûségének mérsékelt csökkenése ellensúlyozni.

A helyzet némiképpen izgalmasabb zárt univerzum esetén. A megfelelôen választott kezdeti feltételek mellett a csillag hômérséklete nagyjából konstans marad az univerzum élete során (6/b.), vagyis az erôsen zárt, rövid élettartamú világegyetemben a csillag energiájának csak kis hányadát sugározza ki. A sugárzási tér hômérséklete mindvégig igen közel marad a csillag hômérsékletéhez, ám eleinte a tágulás következtében kisebb annál, késôbb pedig a kölcsönhatás és az összehúzódás együttes hatására meghaladja azt. Mivel ekkor a fotontér forróbbá válik a csillagnál, a kölcsönhatási folyamatban fellépô hôközlés iránya megfordul: ettôl fogva a fotontér adja át az energiáját a csillagnak, ami viszont (negatív hôkapacitása miatt) ettôl hûlni kezd. Ám a fotontér is hûlni fog, hiszen immár nem hôt kap, hanem hôt közöl. Természetesen a világegyetem összehúzódása ezen hûlés ellenére dolgozik, és a legvégsô viszonyok nagymértékben függenek a kezdeti paraméterektôl.

A 6/b. ábrán az entrópia-görbe igen érdekes alakot vesz fel. Mivel a kölcsönhatás mértéke a hômérsékletek különbségétôl függ, kezdetben viszonylag nagy lesz az entrópiaprodukció, majd a hômérsékletek kiegyenlítôdésekor lecsökken (az egyenlô hômérsékletekkel jellemzett idôpontban persze nullává válik), aztán a hômérsékletek ismételt (immár fordított elôjelû) eltávolodásakor újból megnövekszik, hogy végül megintcsak visszaessen. Megjegyzendô, hogy a 6/a. ábrán az entrópia (és ezzel együtt az összes többi görbe) nem ugyanolyan beosztású skálán került ábrázolásra, mint a 6/b. árbán, hiszen várható, hogy a nyílt univerzum esetében a hômérsékletek különbségének jóval nagyobb értéke sokkal erôteljesebb entrópiaprodukcióhoz vezet, mint a zárt univerzum csekély hômérsékletdifferenciája. A két ábra összehasonlítása csupán minôségi, és nem pedig mennyiségi szempontok alapján lehet jogos.
 

4.2.5. Az RBH-modell és a valódi fekete lyukak

Láthattuk, hogy az ábrázolt speciális termodinamikai rendszerben a negatív hõkapacitás pozitív visszacsatolást teremt hõmérséklet és a kisugárzás között. Amennyiben az univerzum nyílt, tehát biztosan elég hosszú ideig létezik, valamint nem tételezzük fel, hogy a csillag energiatermelése elõbb-utóbb leáll, akkor a “csillag” addig sugároz egyre növekvõ ütemben, amíg minden energiáját le nem adja a fotontérnek, vagyis amíg teljesen el nem “párolog”. Ezzel a folyamattal tehát modellezni lehet a valódi fekete lyukak elpárolgását.

Érdemes megvizsgálni azonban azt az esetet is, amikor a sugárzási tér hõmérséklete nagyobb, mint a belé ágyazott fekete lyuk hõmérséklete. Ekkor, mint azt a fenti szimuláció mutatja, a lyuk nem párolog el, hiszen a befelé irányuló hõáram meghaladja a lyuk sugárzását, vagyis a fekete lyuk tömege folyamatosan nõ, azaz a sugara is nõ, tehát hõmérséklete állandóan csökken. Ennyire “hideg” fekete lyukak a világegyetem jelenlegi korszakában feltehetõleg nem alakulnak ki, ugyanis ha feltesszük, hogy a fekete lyukak a barionos anyag összesûrûsödésekor keletkeznek, akkor szinte bizonyos, hogy az összesûrûsödött anyag sokkal magasabb hõmérsékletre hevül, mint a háttérsugárzás néhány kelvines hõmérséklete.

Ha a korai szakaszokban, amikor a sugárzás és a barionos anyag közti hômérsékletkülönbség nagyobb volt, ilyen képzõdmények kialakulhattak volna, akkor ezek a lyukak ma is jelen lennének (hiszen egyre tovább hûlnének a fotonháttérsugárzás hatására). Ám mivel úgy tûnik, a megfelelõen magas sugárzási hõmérséklettel és emellett megfelelôen alacsony gázhômérséklettel rendelkezõ univerzumban barionos anyag még nem volt jelen, kialakulása után pedig maga a barionos anyag is túl forró volt ahhoz, hogy gravitációs eredetû sûrûsödések létrejöhessenek, az ilyen fekete lyukak létezése felettébb valószínûtlen.

Egy zárt univerzumban azonban talán elképzelhetô lenne, hogy a kontrakciós fázisnak egy olyan késõi szakaszában jöjjön létre egy fekete lyuk, amikor a sugárzási tér hõmérséklete már kellõen magas ahhoz, hogy a még kevésbé felhevült barionos anyag összetömörült anyagcsomójának hõmérsékletét meghaladja, hiszen az összehúzódó világegyetemben a barionos anyag gyorsabban melegszik, mint a fotontér. Ám a hõmérsékletkülönbség csökkenése nem áll szimmetrikus viszonyban a tágulási fázisban tapasztalható hõmérsékletkülönbség-növekedéssel, ugyanis mivel az atomos anyagban végbemenõ termonukleáris reakciók jobban fûtötték az anyagot, mint a sugárzást, és mert a két komponens közti kölcsönhatás a hõmérsékletkülönbség kiegyenlítésére törekedett, a komponensek hômérsékletgörbéi már azelõtt metszik egymást, mielõtt az univerzum akkora méretûre zsugorodna, amekkora méretnél a tágulási fázisban a két komponens szétcsatolódása bekövetkezett. Ezután pedig, ahogy korábbi modellünk mutatta, a gáz nagyobb ütemben és magasabb hômérsékletre hevül, mint a sugárzás. Így ha a tágulási fázis korai szakaszaiban nem jöhettek létre “hideg” fekete lyukak, akkor a kontrakció még kevésbé produkálhat ilyen objektumokat: a fotontér soha nem lehet elég forró a barionos anyag összehúzódásából származó hõmérséklethez képest.
 

4.3. A jövõ

4.3.1. Amit tudni vélünk

Ma a legtöbb kozmológus úgy gondolja, hogy miután a “hiányzó tömeg” fellelésére irányuló évtizedes csillagászati kutatások terméketlennek bizonyultak (legalábbis a kérdésfelvetés szempontjából), az univerzum tömege feltehetôleg alatta van annak a kritikus tömegnek, ami a tágulást visszafordíthatná, vagyis a világegyetem kozmológiai értelemben nyílt. Ám még ha ki is derülne, hogy nem ez a valódi helyzet, az igen valószínûnek tûnik, hogy a tágulás még sokáig tartani fog, hiszen a felfúvódási fázis megközelítôleg euklídeszi szerkezetûvé simította a teret. A hôhalálra vonatkozó kérdés ezért mindenképpen felmerül, és érdemes egy pillantást vetnünk a távoli jövôre.

Minthogy a protonok élettartama meghatározott, a barionos anyag egy hosszú, de véges idõ elteltével el fog tûnni a világegyetembõl, hiszen ezen az idõléptéken mérve azt mondhatjuk, hogy a neutronok bomlása a protonok szétsugárzása utáni szabad állapotban “azonnal” bekövetkezik. Ekkor homogén és izotróp fotongáz fogja kitölteni az univerzumot. Az, hogy jelen lesz-e mellette a szintén egyenletes eloszlású neutrínógáz is, ma még vitatott kérdés, ugyanis a neutrínók stabilitásának problémája nem tekinthetõ megoldottnak Ám mivel a két gáz semmiféle kölcsönhatásban nem áll egymással, az utóbbi kérdésre adott választól függetlenül elkerülhetetlennek tûnik a konklúzió, hogy amennyiben a világegyetem elég hosszú ideig fennáll, benne a hõhalál korszaka kétség kívül be fog köszönteni.
 

4.3.2. A fekete lyukak elpárolgása

A fekete lyukak, lévén gravitációs terükkel meghatározott objektumok, a kozmoszban található minden más anyaggal kölcsönhatásban állnak. Egyelôre még csak kevéssé megalapozott feltételezésekkel élhetünk velük kapcsolatban, de a megfigyelések alapján úgy tûnik, hogy ez a kölcsönhatás ma még nem számottevõ a világegyetem termodinamikai összképének szempontjából. Ám a távoli jövõben, amikor a barionos anyag eltûnik, a fekete lyukak szerepe nagyobb hangsúlyhoz juthat, entrópiájuk igen magas értéket ad. Hiszen az RBH-modell arra az eredményre vezetett, hogy amikor egy fekete lyuk elpárolog, hômérséklete igen magas értékre ugrik fel, és a 6/a. ábráról leolvasható, hogy ez a jelenség szokatlanul komoly mértékû entrópiaprodukciót eredményez.

Egy fekete lyuk entrópiája (Hawking és mások szerint) a pontosabb megfontolások alapján a következõképpen számítható ki:
 


S = (h c5 / 32 p g k) T -2 .


Ha behelyettesítjük az ismert konstansok értékét, láthatjuk, hogy ilyen hatalmas entrópiát egyetlen más (ismert) anyagforma sem tud ekkora hatékonysággal képviselni. Amennyiben tehát a távoli jövõben (nyílt, vagy nem “túlságosan” zárt világegyetemben) a protonok bomlása után a sugárzástól különbözõ anyag már csak fekete lyukak formájában lenne jelen, úgy a fekete lyukak még mindig óriási entrópiát raktároznának, és elpárolgásuk nagyszabású entrópiaprodukcióhoz vezetne, ami megtörné a korábban már esetleg bekövetkezett hôhalál-állapot uralmát (a fotontér egy idôre inhomogénné válna).

Ám Hawking nevezetes eredménye (és az RBH-modell) alapján úgy gondoljuk, hogy a fekete lyukak élettartama is véges, ugyanis az eseményhorizonton bekövetkezõ kvantum-fluktuációknak köszönhetõen a fekete lyukak “párolognak” (és így kerülik el a termodinamika második fõtételének megsértését). Ha a fekete lyukba nem hullik számottevõ mennyiségû anyag vagy sugárzás (mint a távoli jövõ ritka univerzumában), akkor a lyuk Hawking-sugárzáson keresztüli tömegveszteségét semmi sem pótolja. Ez tehát azt jelenti, hogy bár a fekete lyukak sugárzása fûti a világegyetemet betöltõ fotongázt, ez az entrópia-növelõ folyamat is megszûnik idõvel, mert végül a fekete lyukak is eltûnnek majd az univerzumból.
 

4.3.3. Kétségek

Persze semmi sem garantálja azt, hogy a hõhalál fázisa egyben a világegyetem fejlõdésének végsõ fázisa lenne. Még ha fel is tételezzük a természettörvények idõbeli invarianciáját (hiszen ezen feltevés nélkül a hosszú távú jóslatok teljesen lehetetlenné válnának), sosem zárhatjuk ki annak lehetõségét, hogy eddig ismeretlen jelenségek felfedezése módosítani fogja a jövõrõl alkotott képünket. (Ismeretes Landsberg egyik grafikonja, ahol a történelmi idõ függvényében ábrázolta annak az idõtartamnak a logaritmusát, amekkorának a világegyetem korát akkoriban becsülték, és a pontokra egy szép egyenest tudott illeszteni.)

Minél jobban megközelítjük elméleteinkkel az Õsrobbanás pillanatát, annál mélyebb összefüggéseiben sikerül megértenünk a természetet, és annál biztosabban és távolabbra tudunk általánosítani a mai megfigyelések alapján. A jövô tudományos kutatásai során még bizonyára számos meglepetés fog érni bennünket. Elképzelhetõ, hogy kiderül, hogy a világegyetem anyagának ismert vagy ismeretlen része (lásd a sötét anyag megoldatlan problémáját) újabb lecsatolódást fog megvalósítani, vagy maga a vákuumtér megy majd keresztül egy következõ fázistranszformáción, lehetõséget teremtve nagymennyiségû szabadenergia keletkezésére. Egyes újabb elméletek szerint a vákuumpotenciál értéke még ma sem nulla, ezért a vákuum lassan egyre lejjebb kerül a potenciálfüggvénye mentén, ami viszont azt jelenti, hogy a ritkuló anyag csökkenô gravitációs effektusai alól felszabadulva a vákuum ismét egy gyorsuló tágulást okozhat a jövôben, vagy akár már a jelenben is: ennek a felfúvódásnak a végét a mai elméletek egyáltalán nem tudják elôrejelezni.

Végeredményben úgy tûnik, hogy a hõhalál fogalma egy merõben képlékeny fogalom, ami nem annyira az univerzum jövõjére vonatkozik, mint inkább csupán elméleteink határát jelzi.


 

Függelékek

A. Függelék: A modell-világegyetem termodinamikája

A következõ levezetés Marx Györgynek és az õ forrásainak megfontolásait követi.

Idézzük emlékezetünkbe ismét a két Einstein-egyenletet:
 
 ,
(1)
.
(2)

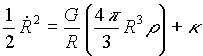Tételezzük fel, hogy a sugárzásra és a gázokra vonatkozó néhány alapvetõ összefüggést figyelembe véve, az univerzum teljes energiatartalma a következõképpen írható (a természetes mértékegység-rendszerben):
 
E = c1 R3Tr4 + B (m + 3/2 Tg) ,
(3)

ahol c1 egy konstans, B a barionszám (a gázrészecskék száma) és m a gázrészecskék tömege. Ekkor az egyes komponensek hõkapacitását könnyedén megkaphatjuk:
 
,
(4)
.
(5)

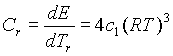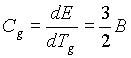A termodinamika elsõ fõtétele a következõ formákban írható fel:
 
,
(6)
.
(7)

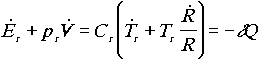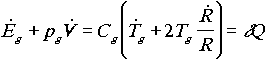Feltesszük, hogy a hõáram az alábbi alakban fejezhetõ ki:
 
,
(8)

ahol A a kölcsönhatás erõségére jellemzõ paraméter.

Az (1), (4), (5), (6), (7), (8) egyenletekbõl álló rendszer meghatározza a modell-univerzum idõbeli fejlõdését. A differenciálegyenlet-rendszer ilyen formára hozható:
 
,
(9)
,
(10)
.
(11)

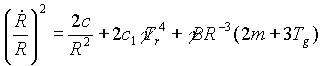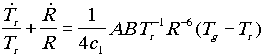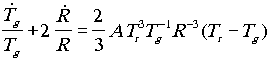Minthogy az entrópia megváltozása:
 
,
(12)

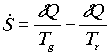ezt összevetve a (8) egyenlettel azt kapjuk, hogy  kifejezése így alakítható tovább:
 
.
(13)

Végül tehát a (9), (10), (11) és (13) egyenletek megoldására van szükségünk ahhoz, hogy a 2. és 4. ábrasorozatok bal oldali ábráit elkészíthessük.

Az egyenletrendszer megoldásához és az eredmények ábrázolásához a Mathematica nevû programot használtam.
 

B. Függelék: A világegyetem extrópiájának kifejezése

Az univerzumot egy adott állapotában jellemzõ extrópiát felfoghatjuk úgy is, mint annak az entrópiának a mennyiségét, amit a világegyetem akkor termelne, ha rögzített extenzív paraméterek mellett a kérdéses állapotból termikus egyensúlyba jutna. Minthogy ebben a folyamatban a modellünk hidegebb anyagkomponense teljes egészében felvenné a melegebb komponens által leadott hõt, a folyamat a következõ egyenlettel jellemezhetõ:
 
,
(14)

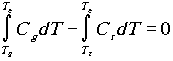ahol Cg és Cr értékét meghatározzák a (4) és (5) egyenletek. Te az az egyensúlyi hõmérséklet, amit a két komponens közösen felvenne az egyensúly állapotában. Ha az egyszerûség kedvéért feltesszük, hogy a hõkapacitások ekkora hõmérséklet-tartományban állandónak tekinthetõk (ami Cg esetén teljesül is, és csupán Cr esetében követel meg némi jóindulatot), akkor az egyszerû integrálás eredményeképpen:
 
.
(15)

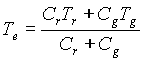Mivel az extrópia a folyamatban termelt entrópiával azonosítható, valamint munkavégzés híján dE = dQ :
 
,
(16)

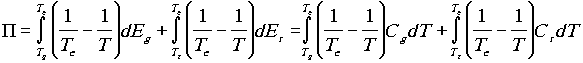és a hõkapacitásokat továbbra is állandónak tartva azt kapjuk, hogy
 
.
(17)

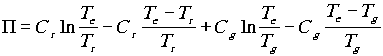Ezen összeg második és negyedik tagja a (15) egyenlet alapján összevonva nullát ad, így az extrópia kifejezése még tovább alakítható:
 
,
(18)

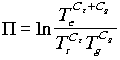amibe ha behelyettesítjük a Te (15) egyenletben kapott kifejezését, akkor némi egyszerûsítések után azt a nem annyira egyszerû képletet kapjuk, hogy:
 
,
(19)

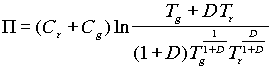ahol 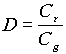 . Tekintsük ezt az extrópia végsõ kifejezésének, minthogy az ábrázolás során is ezt a képletet használtam a számításokhoz.
 

C. Függelék: Az univerzum sugarának fejlõdése

Tekintsük ismét az (1) Einstein-egyenletet, ám a tömegsûrûség helyett dolgozzunk most az energiasûrûséggel: u = r c2 . Vegyük az egyenlet deriváltját:
 
,
(20)

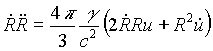ami természetesen már független az univerzum metrikájára jellemzõ k konstanstól, ami a deriváláskor eltûnt. kifejezéséhez elõször is vegyük figyelembe, hogy amennyiben a térfogat: V = b R3 (b valami konstans együttható), akkor
 
,
(21)

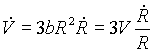ami felhasználható az energia deriváltjának kifejezésében:
 
.
(22)

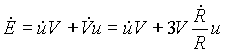Másfelõl, adiabatikus folyamat esetén az energia deriváltja termodinamikailag így írható:
 
.
(23)

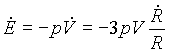Összevetve a (22) és a (23) egyenletet, kifejezhetõ a következõképpen:
 
,
(24)

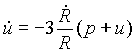amit a (20) egyenletbe írva a tágulás sebességének változása végül erre a formára hozható:
 
.
(25)

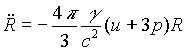Nem csoda tehát, hogy normál fizikai paraméterek mellett a tágulás üteme lassul, ám amennyiben a felfúvódási fázisban , ilyenkor a világegyetem tágulása gyorsul.
 

D. Függelék: A sugárzási térbe ágyazott fekete lyuk termodinamikája

Ismét Marx György logikáját követve, a 4.2.3. alfejezetben levezetett eredményeket itt csupán néhány kiegészítéssel kell megtoldanunk.

A fekete lyukkal modellezett csillag és az õt magába ágyazó fotontér termodinamikai rendszere a következõ egyenletekkel határozható meg:
 
,
(26)
,
(27)

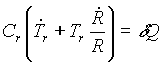ahol Cr és Cs a fotontér, illetve a fekete lyuk hõkapacitása: az elsõt a (4) egyenletben már kifejeztük, a másodikat pedig a megfelelõ alfejezetben határoztuk meg:
 
.
(28)

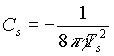Figyelembe véve az (1) Einstein-egyenletet, a fentiek alapján a következõ differenciálegyenlet-rendszert kapjuk:
 
,
(29)
,
(30)
.
(31)

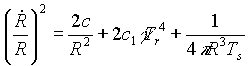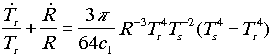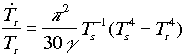Annak feltételezése mellett, hogy az égitestet elhagyó sugárzás igen hamar a környezõ sugárzási tér megkülönböztethetetlen részévé válik, az entrópia megváltozásának a szövegben említett kifejezéséhez jutunk:
 
.
(32)

E négy utóbbi egyenlet rendszerének megoldásával juthatunk el az 6. ábra megalkotásához.


 

Források és hivatkozások
 
 
Alpher, R.A. & Marx, Gy.:
The creation of free energy
Vistas in Astronomy, Vol. 35 (1992)
 
Brodszky, I. & Martinás, K.:
Az integráló-osztó története
Fizikai Szemle, 44/324 (1997)
 
Carathéodory, C.:
Untersuchungen über die Grundlagen der Therodynamik
Mathematische Annalen, Vol. 67 (1909)
 
Clausius, R.:
Abbandlungen über die mechanische Wä rmetheorie I.
Vieweg und Sohn, Braunschweig, 1864
 
Davies, P.:
Az utolsó három perc
Kultúrtrade, 1994.
 
Diósi, L. & Lukács, B. & Martinás, K. & Paál, G.:
On the thermodynamics of the vacuum
Astrophysics and Space Science, Vol. 122 (1986)
 
Erdei, A. & Martinás, K.:
Farkas Gyula új termodinamika-felépítése
Fizikai Szemle, 44/328 (1997)
 
Farkas, Gy.:
A Carnot-Clausius féle tétel egyszerûsített levezetése
Mathematikai és Physikai Lapok, IV. (1895)
 
Guth, A. & Steinhardt, P.: 
The inflationary universe 
Scientific American, May 1984
 
Hawking, S.W.:
The no-boundary proposal and the arrow of time
Vistas in Astronomy, Vol. 37 (1993)
 
Hawking, S.W.:
Az idõ rövid története
Maecenas, 1988
 
Imre, A. & Martinás, K. & Rebelo, L.P.N.:
Thermodynamics of negative pressures in liquids
Journal of non-equilibrium thermodynamics, Vol. 23. (1998)
 
Landsberg, P.T.:
The physical concept of time in the 20th century
in: Physics in the making; eds.: Sarlemijn, A & Sparnaay, M.J., Elsevier, 1989
 
Landsberg, P.T.:
From entropy to God?
in: Thermodynamics: History and Philosophy; papers from the July 1990 
conference in Veszprém
 
Lukács, B. & Martinás, K. & Pacher, T.:
Extended thermodynamics in the early universe
Astronomische Nachr., vol. 307. (1986)
 
Lukács, B.:
On heat death in past, present or future
Acta Climatologica, 24/16/1-4. (1992)
 
Martinás, K. & Ropolyi, L.:
Antik termodinamika
Fizikai Szemle, 45/418 (1988)
 
Martinás, K.:
Information and Entropy
World Futurum, Vol. 49. (1997)
 
Marx, Gy.: 
Irreverzibilis univerzum 
Fizikai Szemle, 38/162 (1988)
 
Nagy, K.: 
Termodinamika és statiszikus mechanika 
Tankönyvkiadó, Budapest, 1991
 
Peebles, P.J.E.:
Evolution of the cosmological constant
Nature, Vol. 398 (1999)
 
Simonyi, K.:
A fizika kultúrtörténete
Gondolat, Budapest, 1984
 
Székely, L.:
Einstein kozmoszától a fölfúvódó világegyetemig
A Filozófiai Figyelõ kiskönyvtára, Budapest, 1990
 
Truesdell, C.:
Failure of Carathéodory's attempt to set the house in order
in: Ratonal Thermodynamics, Springer-Verlag, 1984
 
Voigt, W.:
Kompendium der theoretischen Physik
Verlag von Veit u. Comp., Leipzig. I. Band. 1895. II. Band. 1896
 
Zeuner, G.:
Grundzüge der mechanischen Wä rmetheorie
Zweite Auflage 1866. Neuer Abdruck, Leipzig, 1877